Integral Of 1 X 2 1 2
Greels
Apr 01, 2025 · 5 min read
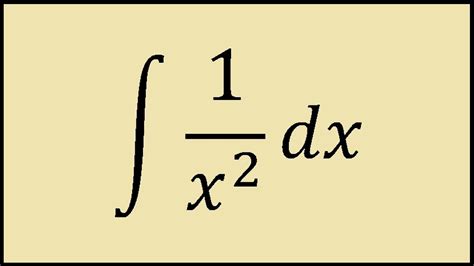
Table of Contents
Decoding the Integral: A Comprehensive Exploration of ∫(1/(x²+1))dx
The seemingly simple integral, ∫(1/(x²+1))dx, holds a significant place in calculus and its applications. While its solution might appear straightforward, a deep dive into its derivation, properties, and applications reveals a richness often overlooked. This article will explore this integral comprehensively, delving into its solution, its connection to trigonometric functions, and its far-reaching implications in various fields.
Understanding the Integral: A Starting Point
Before diving into the solution, let's clarify what this integral represents. The expression ∫(1/(x²+1))dx denotes the indefinite integral of the function f(x) = 1/(x²+1). In simpler terms, we're searching for a function whose derivative is 1/(x²+1). This integral is a fundamental building block in calculus, appearing frequently in diverse mathematical contexts.
Solving the Integral: The Arctangent Function
The solution to this integral involves the arctangent function, often denoted as arctan(x) or tan⁻¹(x). The arctangent function is the inverse function of the tangent function, meaning it returns the angle whose tangent is a given value. Specifically:
∫(1/(x²+1))dx = arctan(x) + C
where 'C' is the constant of integration. This constant is crucial because the derivative of a constant is zero. Therefore, any constant added to the arctangent function will still have a derivative of 1/(x²+1).
Proving the Solution: Differentiation
To verify the solution, we can differentiate arctan(x) and demonstrate that its derivative indeed equals 1/(x²+1). This verification is paramount in confirming the accuracy of our integral. The derivative of arctan(x) is derived using the inverse function theorem, a powerful tool in calculus. The process involves implicit differentiation, leading to the result:
d/dx[arctan(x)] = 1/(x²+1)
This confirms that our solution, arctan(x) + C, is indeed the correct indefinite integral of 1/(x²+1).
Applications of the Integral: Beyond the Textbook
The seemingly simple integral ∫(1/(x²+1))dx has surprisingly diverse applications across various fields. Its presence extends beyond theoretical mathematics and finds practical utility in engineering, physics, and computer science.
1. Probability and Statistics: Normal Distribution
The arctangent function, directly related to our integral, plays a crucial role in the calculation of probabilities related to the normal distribution. The normal distribution, a ubiquitous probability distribution, is used extensively in statistics to model various phenomena, from heights and weights to exam scores. Integrals involving 1/(x²+1) are involved in deriving cumulative probabilities under the normal curve.
2. Physics: Electric Potential and Fields
In electrostatics, the integral ∫(1/(x²+1))dx arises when calculating electric potential due to certain charge distributions. Understanding the electric potential is crucial in various electrical engineering applications and in studying the behavior of charged particles. The arctangent function, a direct result of the integral, provides a direct method to determine the electric potential at different points in space.
3. Engineering: Signal Processing and Control Systems
The integral finds its way into signal processing and control systems engineering. Applications include designing filters, analyzing signals, and modeling dynamic systems. These applications often involve Laplace transforms, a mathematical technique deeply reliant on integration. The integral of 1/(x²+1) appears as a component in many Laplace transform solutions.
4. Computer Science: Numerical Integration and Algorithm Design
Numerical methods for approximating integrals are critical in computer science. Approximating the integral of 1/(x²+1) often serves as a test case for developing and evaluating the accuracy of numerical integration algorithms. This helps computer scientists assess and refine the performance of their computational methods.
Exploring Related Integrals: Variations and Extensions
Understanding ∫(1/(x²+1))dx opens the door to understanding a broader family of integrals. By employing techniques like substitution and partial fractions, we can solve more complex integrals related to this basic form.
1. Integrals with Scaling and Shifting: ∫(1/(a²x²+1))dx
Introducing a scaling factor 'a' in the denominator leads to the integral ∫(1/(a²x²+1))dx. This integral can be solved using a simple substitution, revealing a scaled version of the arctangent function as its solution:
∫(1/(a²x²+1))dx = (1/a)arctan(ax) + C
2. Integrals with a Constant Term in the Denominator: ∫(1/(x²+a²))dx
Adding a constant term 'a²' to the denominator results in the integral ∫(1/(x²+a²))dx. A similar substitution technique yields:
∫(1/(x²+a²))dx = (1/a)arctan(x/a) + C
3. Integrals Involving Partial Fractions: More Complex Denominators
More complex integrals involving rational functions (ratios of polynomials) in the denominator can often be solved using partial fraction decomposition. This technique breaks down the rational function into simpler fractions, each of which can then be integrated using techniques similar to those used for the basic integral.
Conclusion: A Fundamental Building Block
The integral ∫(1/(x²+1))dx, seemingly uncomplicated at first glance, serves as a fundamental building block in calculus and beyond. Its solution, the arctangent function, has wide-ranging applications in probability and statistics, physics, engineering, and computer science. Understanding this integral and its extensions lays a solid foundation for tackling more complex integration problems and for appreciating the profound power of calculus in solving real-world problems. Its seemingly simple nature belies the crucial role it plays in a vast array of mathematical and scientific disciplines. The exploration of this integral highlights the beauty and elegance of mathematics, demonstrating how seemingly simple concepts can have far-reaching implications and contribute to a deeper understanding of our world. This integral serves as a prime example of the interconnectedness of mathematical concepts and their critical role in unlocking the secrets of the universe. Furthermore, mastering this integral and its variations is crucial for anyone seeking proficiency in advanced mathematical concepts and their practical applications. The journey from a simple integral to its diverse applications underscores the beauty and utility of mathematical analysis.
Latest Posts
Latest Posts
-
How Many Inches Is 44 Centimeters
Apr 02, 2025
-
How Many Inches Is 49 Mm
Apr 02, 2025
-
What Date Was 300 Days Ago
Apr 02, 2025
-
9 K 4 7k 32 2 K 8
Apr 02, 2025
-
How Long Is 40 Inches In Cm
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
