How Much Is 30 Of 200
Greels
Apr 23, 2025 · 4 min read
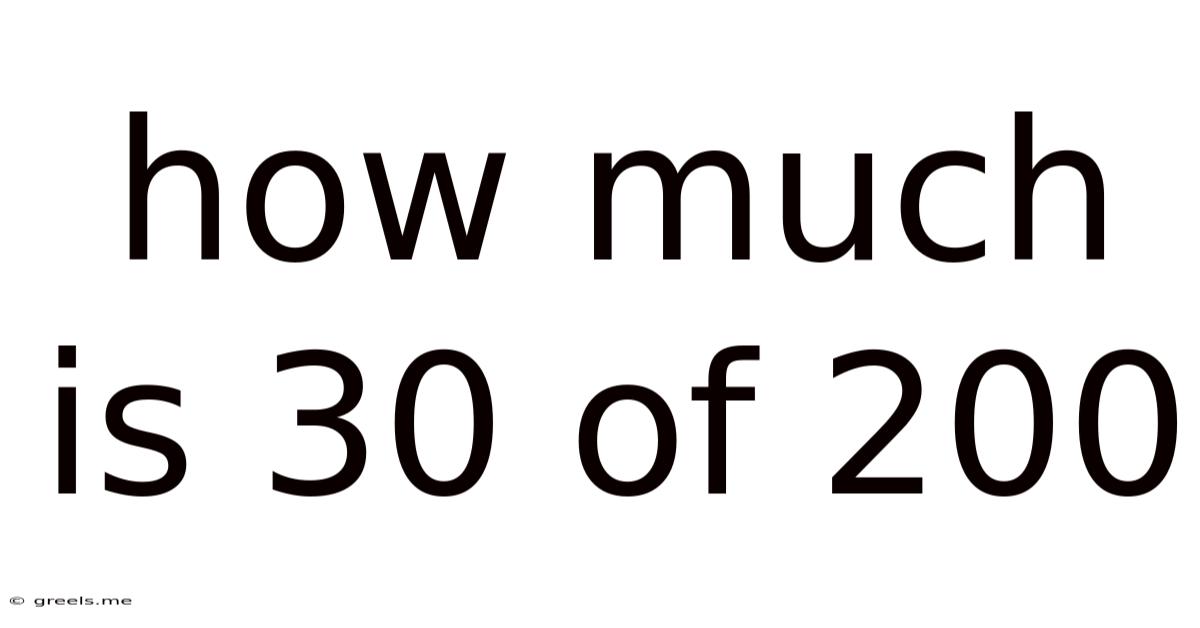
Table of Contents
Decoding Percentages: A Deep Dive into "How Much is 30% of 200?"
This seemingly simple question, "How much is 30% of 200?", opens the door to a world of percentage calculations, their practical applications, and the underlying mathematical concepts. While the answer itself is straightforward, understanding the how and why behind the calculation empowers you to tackle more complex percentage problems with confidence. This comprehensive guide will not only provide the solution but also explore the different methods for calculating percentages, their relevance in various fields, and how to improve your overall understanding of this fundamental mathematical concept.
Understanding Percentages: The Foundation
Before diving into the calculation, let's establish a solid understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per cent" or "out of 100". Therefore, 30% can be written as 30/100 or 0.30 in decimal form. This fundamental understanding is crucial for tackling any percentage problem.
Method 1: Using the Formula
The most common and straightforward method to calculate a percentage of a number involves a simple formula:
(Percentage/100) * Number = Result
In our case:
(30/100) * 200 = 60
Therefore, 30% of 200 is 60. This formula is universally applicable for any percentage calculation. You can substitute any percentage and number to find the desired result.
Method 2: Decimal Conversion
Converting the percentage to a decimal offers an alternative approach. As mentioned earlier, 30% is equivalent to 0.30. Therefore, the calculation becomes:
0.30 * 200 = 60
This method streamlines the process, especially when dealing with larger numbers or performing calculations mentally. It demonstrates the direct relationship between percentages and decimals.
Method 3: Proportion Method
This method utilizes the concept of proportionality. We can set up a proportion to solve for the unknown value (x):
30/100 = x/200
To solve for x, we cross-multiply:
30 * 200 = 100 * x
6000 = 100x
x = 6000/100 = 60
This method reinforces the understanding of percentages as ratios and provides a systematic approach for solving percentage problems, particularly useful when dealing with more complex scenarios.
Practical Applications: Where Percentages Matter
Understanding percentage calculations is crucial across numerous fields:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all heavily rely on percentage calculations. For example, understanding the interest rate on a loan or the discount on a product requires accurate percentage calculations.
-
Retail: Businesses use percentages to determine discounts, markups, and sales tax. Knowing how to calculate these percentages helps businesses set prices competitively and manage profitability.
-
Science: Percentage calculations are essential in data analysis, representing proportions in experiments, and expressing concentrations of substances.
-
Everyday Life: Calculating tips in restaurants, understanding sale discounts, and interpreting statistics in news reports all involve percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating 30% of 200 is relatively simple, let's explore more complex scenarios to enhance our understanding:
Scenario 1: Finding the Percentage: If you know the part and the whole, you can calculate the percentage. For instance, if 60 is a part of 200, what percentage is it?
60/200 * 100 = 30%
Scenario 2: Finding the Whole: If you know a percentage and the part, you can calculate the whole. For example, if 60 represents 30% of a number, what is the whole number?
60/0.30 = 200
Mastering Percentage Calculations: Tips and Tricks
-
Practice regularly: The key to mastering any mathematical concept is consistent practice. Try solving various percentage problems with different numbers and scenarios.
-
Use online calculators: Online calculators can be helpful for checking your work and understanding different methods. However, always aim to understand the underlying principles, not just rely on the calculator.
-
Break down complex problems: Large and complicated problems can be simplified by breaking them into smaller, manageable steps.
-
Visual aids: Diagrams, charts, and graphs can help visualize percentages and make understanding easier.
-
Understand the context: Always pay attention to the context of the problem to ensure you are applying the correct method and interpreting the results correctly.
Conclusion: The Power of Percentage Understanding
The seemingly simple question, "How much is 30% of 200?" reveals the importance and wide applicability of percentage calculations. Mastering these calculations not only improves mathematical skills but also equips individuals with practical tools for navigating various aspects of daily life, finance, and professional fields. By understanding the different methods, practicing regularly, and appreciating the practical context, one can confidently tackle any percentage problem and unlock its power in various real-world applications. The journey from understanding the basics to tackling complex scenarios is a testament to the power of consistent learning and application. Remember, the ability to confidently calculate percentages is a valuable asset in today's world.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Much Is 30 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.