Factor X 3 3x 2 X 3
Greels
Apr 05, 2025 · 4 min read
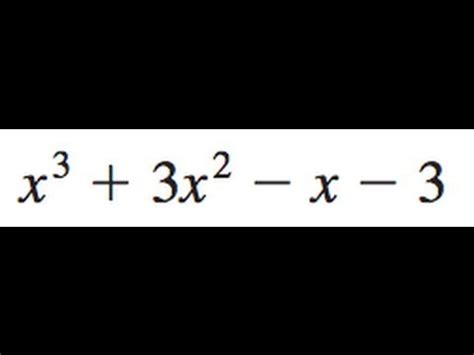
Table of Contents
Factoring the Cubic Polynomial: x³ + 3x² + x - 3
Factoring polynomials is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding the behavior of functions. While factoring quadratic expressions is relatively straightforward, factoring higher-degree polynomials, such as cubics (polynomials of degree three), can be more challenging. This article delves into the process of factoring the specific cubic polynomial, x³ + 3x² + x - 3, exploring various techniques and providing a comprehensive understanding of the steps involved. We'll explore both numerical and graphical methods to fully analyze this polynomial.
Understanding the Problem: x³ + 3x² + x - 3
Our objective is to find the factors of the cubic polynomial x³ + 3x² + x - 3. This means we're looking for expressions, when multiplied together, that result in this original polynomial. The factors might be linear (degree one) or quadratic (degree two) expressions. There are several approaches we can use to achieve this factorization.
The Rational Root Theorem: A Starting Point
One powerful tool for factoring polynomials is the Rational Root Theorem. This theorem states that any rational root (a root that can be expressed as a fraction p/q, where p is a factor of the constant term and q is a factor of the leading coefficient) of a polynomial must be of this form.
In our polynomial, x³ + 3x² + x - 3:
- The constant term is -3. Its factors are ±1 and ±3.
- The leading coefficient is 1. Its factors are ±1.
Therefore, the possible rational roots are ±1 and ±3. We can test these values by substituting them into the polynomial:
- If x = 1: 1³ + 3(1)² + 1 - 3 = 2 ≠ 0
- If x = -1: (-1)³ + 3(-1)² + (-1) - 3 = -2 ≠ 0
- If x = 3: 3³ + 3(3)² + 3 - 3 = 54 ≠ 0
- If x = -3: (-3)³ + 3(-3)² + (-3) - 3 = -27 + 27 - 6 = -6 ≠ 0
None of these possible rational roots are actual roots. This suggests that the polynomial may not have any rational roots, or that it may have irrational or complex roots. This necessitates exploring alternative methods.
Exploring Alternative Factoring Techniques
Since the rational root theorem didn't yield any roots, let's explore other approaches:
1. Grouping Method: A Potential Strategy (But Unsuccessful Here)
The grouping method involves attempting to group terms within the polynomial to find common factors. Let's try this with our polynomial:
x³ + 3x² + x - 3
We can try grouping in several ways, but none lead to a straightforward factorization. This indicates that a different approach is necessary.
2. Polynomial Long Division: Utilizing a Known Factor (If Available)
If we knew one factor of the polynomial, we could use polynomial long division to find the other factor. However, we haven't found a rational factor. This method requires prior knowledge of at least one root or factor.
3. Numerical Methods: Approximating Roots
Since the rational root theorem proved fruitless, we can resort to numerical methods. These methods use iterative processes to approximate the roots of the polynomial. Common methods include:
- Newton-Raphson Method: This iterative method uses the derivative of the polynomial to refine an initial guess towards a root.
- Bisection Method: This method repeatedly bisects an interval containing a root, narrowing down the search until a desired accuracy is achieved.
These methods, while powerful, require iterative calculations and are typically best suited for implementation using computational tools like calculators or programming software. They would yield approximate values for the roots, rather than exact expressions.
4. Graphical Analysis: Visualizing the Roots
A graphical approach can provide valuable insights. By plotting the function y = x³ + 3x² + x - 3, we can visually identify the approximate locations of the x-intercepts (where y = 0), which correspond to the roots of the polynomial.
Using graphing software or a calculator, you'll observe that the graph intersects the x-axis at approximately one point between -2 and -1, and another at approximately one point between 0 and 1. The exact values are irrational. The graph visually confirms that there are no integer or simple rational roots. This aligns with our previous findings using the Rational Root Theorem.
Interpreting the Results and Further Analysis
The lack of easily identifiable rational roots indicates that the factors of x³ + 3x² + x - 3 likely involve irrational or complex numbers. Finding these factors analytically can be quite involved and often requires advanced techniques like using Cardano's method for solving cubic equations. This method involves complex algebraic manipulations and is beyond the scope of a general introductory algebra discussion.
Conclusion: The Challenges and Implications
Factoring the cubic polynomial x³ + 3x² + x - 3 demonstrates the challenges involved in factoring higher-degree polynomials. While techniques like the Rational Root Theorem and grouping can be helpful, they are not universally successful. Numerical and graphical methods provide alternative approaches, offering approximate solutions when analytical methods prove intractable. The fact that this specific polynomial does not readily factor into simple rational expressions highlights the importance of understanding the limitations of elementary factoring techniques and the need for more advanced methods when dealing with complex polynomials. The existence of irrational or complex roots is perfectly normal and a common occurrence in higher-degree polynomial analysis. The absence of simple factors doesn't imply there’s a problem with the polynomial; it simply indicates the nature of its roots.
Latest Posts
Latest Posts
-
2x 2 4x 3 6 6x
Apr 06, 2025
-
Cuanto Es 7 5 Pulgadas En Cm
Apr 06, 2025
-
How Long Is 45cm In Inches
Apr 06, 2025
-
134 Inches Is How Many Feet
Apr 06, 2025
-
200 Miles Per Hour To Km
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Factor X 3 3x 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
