Factor X 2 Xy Y 2
Greels
Apr 23, 2025 · 5 min read
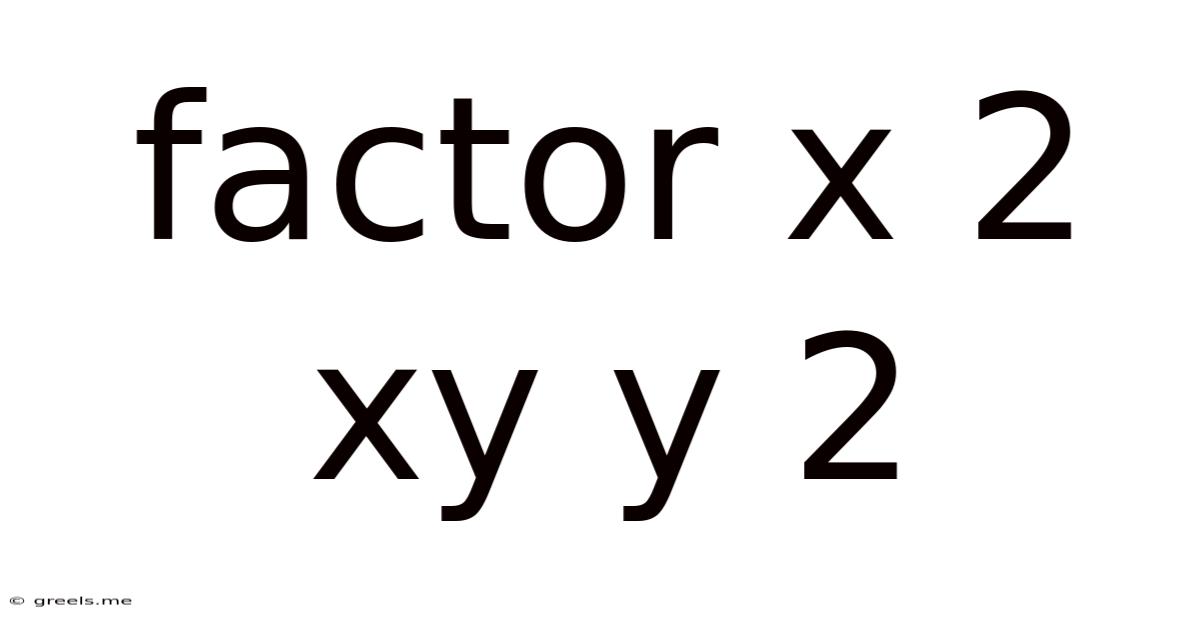
Table of Contents
Understanding the Factor x² + 2xy + y²: A Complete Guide
The expression x² + 2xy + y² is a fundamental concept in algebra, appearing frequently in various mathematical contexts. Understanding its factorization is crucial for simplifying expressions, solving equations, and grasping more advanced algebraic concepts. This comprehensive guide will delve into the intricacies of this expression, exploring its factorization, applications, and related topics.
What is x² + 2xy + y²?
x² + 2xy + y² is a trinomial, meaning it's a polynomial with three terms. Each term is a product of variables (x and y) raised to certain powers and possibly multiplied by a constant. Specifically, this trinomial is a perfect square trinomial, a special type of trinomial that can be factored easily.
Factoring x² + 2xy + y²: The Perfect Square Trinomial
The key to understanding this expression lies in recognizing its structure as a perfect square trinomial. This means it can be expressed as the square of a binomial. The factorization is:
(x + y)² = x² + 2xy + y²
This factorization can be derived using the FOIL method (First, Outer, Inner, Last) for expanding binomials:
(x + y)(x + y) = x² + xy + xy + y² = x² + 2xy + y²
Therefore, the square root of x² + 2xy + y² is (x + y). This is a crucial piece of information for many algebraic manipulations.
Understanding the Pattern
The pattern of a perfect square trinomial is consistently observed:
- The first term (x²) is the square of one term in the binomial (x).
- The last term (y²) is the square of the other term in the binomial (y).
- The middle term (2xy) is twice the product of the two terms in the binomial (2 * x * y).
Recognizing this pattern is key to quickly identifying and factoring perfect square trinomials. This ability is essential for solving quadratic equations and simplifying complex algebraic expressions.
Applications of Factoring x² + 2xy + y²
The factorization of x² + 2xy + y² has numerous applications in various mathematical fields. Here are some key examples:
1. Solving Quadratic Equations
Many quadratic equations can be simplified and solved more easily by factoring them into perfect square trinomials. For example, consider the equation:
x² + 6x + 9 = 0
This equation can be factored as (x + 3)² = 0, leading to a simple solution of x = -3.
2. Simplifying Algebraic Expressions
The factorization simplifies complex algebraic expressions. Consider:
(x² + 2xy + y²) / (x + y)
By factoring the numerator as (x + y)², the expression simplifies to (x + y). This simplification significantly reduces the complexity of the expression, making further calculations easier.
3. Geometry and Area Calculations
The expression can represent the area of a geometric figure. If x and y represent the sides of a square, then x² + 2xy + y² represents the area of a larger square formed by adding a rectangle with sides x and y to the original square with side x. The factorization (x+y)² illustrates that this larger area is simply the square of the sum of the two sides.
4. Calculus
In calculus, factoring perfect square trinomials is frequently used in simplifying derivatives and integrals. This simplification can make the integration or differentiation process significantly easier and more manageable.
Variations and Related Expressions
While x² + 2xy + y² is the most common form, understanding variations and related expressions is crucial for broader algebraic proficiency:
1. x² - 2xy + y²
This expression is also a perfect square trinomial, but with a negative middle term. Its factorization is:
(x - y)² = x² - 2xy + y²
Notice the subtle but significant difference: the binomial is now (x - y), leading to a negative middle term in the expansion.
2. ax² + 2axy + ay²
This is a generalization of the original expression. It incorporates a constant 'a', which can be factored out:
a(x² + 2xy + y²) = a(x + y)²
The fundamental perfect square trinomial pattern remains intact, even with the addition of the constant factor.
3. Expressions with Different Coefficients
While the expressions above involve straightforward coefficients of 1 and 2, other perfect square trinomials exist. Consider:
4x² + 12xy + 9y²
This can be factored as (2x + 3y)², demonstrating that the basic principle of perfect square trinomials applies even when coefficients are not simply 1 and 2. Recognizing the pattern requires identifying the square root of each perfect square term and verifying that the middle term is twice the product of the square roots.
Advanced Applications and Extensions
The concept of perfect square trinomials and their factorization extends far beyond elementary algebra. It plays a critical role in:
1. Complex Numbers
The same factoring principles can be applied to expressions involving complex numbers. The square of a complex number (a + bi)² can be easily expanded and factored using similar techniques.
2. Linear Algebra
In linear algebra, these techniques are relevant in matrix manipulations and solving systems of linear equations. The structure of a perfect square trinomial can sometimes reveal underlying relationships within matrices.
3. Polynomial Equations of Higher Degree
While the examples above focus on quadratic equations, the concept of factoring and identifying patterns extends to polynomial equations of higher degree. Recognizing patterns in higher-degree polynomials can simplify their solutions significantly.
Troubleshooting Common Mistakes
When factoring perfect square trinomials, some common mistakes can lead to incorrect results. Be aware of these:
1. Incorrect Signs
Carefully consider the signs of each term. A negative middle term implies a difference of squares or a binomial with subtraction. Incorrect signs can lead to completely different factorization results.
2. Ignoring Coefficients
Don't forget to account for coefficients that are not equal to one. Factor them correctly to obtain the accurate binomial factorization.
3. Assuming All Trinomials are Perfect Squares
Not all trinomials are perfect squares. Always verify that the pattern fits before attempting to factor as a perfect square.
Conclusion
Understanding the factorization of x² + 2xy + y² is a fundamental skill in algebra. Recognizing the perfect square trinomial pattern, its variations, and its applications across various mathematical areas is crucial for success in more advanced mathematical studies. This guide has provided a thorough exploration of this concept, equipping you with the knowledge and tools to handle related expressions confidently and efficiently. Practicing these factorization techniques is key to mastering this important algebraic concept. Remember to meticulously check your work and be aware of common mistakes to ensure accurate factorization.
Latest Posts
Related Post
Thank you for visiting our website which covers about Factor X 2 Xy Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.