Exact Values Of Trig Functions Calculator
Greels
Apr 01, 2025 · 5 min read
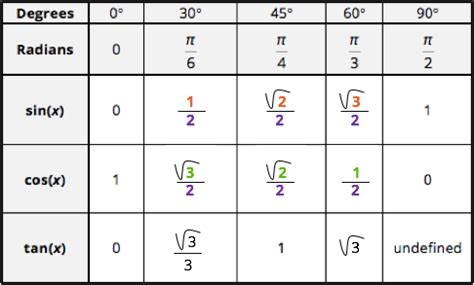
Table of Contents
Exact Values of Trig Functions Calculator: A Comprehensive Guide
Determining the exact values of trigonometric functions is a crucial skill in mathematics, particularly in calculus, trigonometry, and precalculus courses. While calculators provide approximate decimal values, understanding how to calculate exact values is essential for a deeper grasp of trigonometric identities and their applications. This article explores the methods for calculating exact values of trigonometric functions for various angles, focusing on the importance of the unit circle and special triangles. We'll also discuss the limitations of calculators and why understanding the underlying principles is vital.
Understanding the Unit Circle
The unit circle is a circle with a radius of 1 centered at the origin (0,0) of a coordinate plane. It's a fundamental tool for understanding trigonometric functions because it visually represents the relationship between angles and their corresponding sine, cosine, and tangent values.
Coordinates and Trig Functions
Each point on the unit circle has coordinates (x, y). These coordinates directly correspond to the cosine and sine of the angle formed by the positive x-axis and a line segment from the origin to that point. Specifically:
- cos θ = x
- sin θ = y
The tangent of the angle is then calculated as the ratio of sine to cosine:
- tan θ = sin θ / cos θ = y / x
Understanding this relationship allows us to determine the exact values of trigonometric functions for various angles directly from the unit circle's geometry.
Special Angles on the Unit Circle
Certain angles hold particular importance due to their simple and easily calculated trigonometric values. These are commonly referred to as "special angles," and they are derived from 30-60-90 and 45-45-90 right-angled triangles.
30-60-90 Triangle
A 30-60-90 triangle has angles of 30°, 60°, and 90°. The sides are in the ratio 1 : √3 : 2. This allows us to determine exact values for sine, cosine, and tangent of 30° and 60°.
-
30° (π/6 radians):
- sin 30° = 1/2
- cos 30° = √3/2
- tan 30° = 1/√3 = √3/3
-
60° (π/3 radians):
- sin 60° = √3/2
- cos 60° = 1/2
- tan 60° = √3
45-45-90 Triangle (Isosceles Right Triangle)
A 45-45-90 triangle has angles of 45°, 45°, and 90°. Its sides are in the ratio 1 : 1 : √2. This gives us exact values for 45° (π/4 radians):
- 45° (π/4 radians):
- sin 45° = 1/√2 = √2/2
- cos 45° = 1/√2 = √2/2
- tan 45° = 1
Beyond the Special Angles: Using Trigonometric Identities
While the unit circle and special triangles provide exact values for certain angles, we need trigonometric identities to calculate exact values for other angles. These identities establish relationships between different trigonometric functions.
Key Trigonometric Identities
Several identities are crucial for calculating exact values:
-
Pythagorean Identity: sin²θ + cos²θ = 1. This identity is fundamental and allows us to find one trigonometric function if we know the other.
-
Sum and Difference Identities: These identities allow us to express the trigonometric functions of the sum or difference of two angles in terms of the trigonometric functions of the individual angles. For example:
- sin(A + B) = sin A cos B + cos A sin B
- cos(A + B) = cos A cos B - sin A sin B
- tan(A + B) = (tan A + tan B) / (1 - tan A tan B)
-
Double Angle Identities: These are special cases of the sum identities where A = B.
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos²θ - sin²θ = 1 - 2sin²θ = 2cos²θ - 1
- tan 2θ = 2 tan θ / (1 - tan²θ)
-
Half Angle Identities: These identities allow us to find the trigonometric functions of half an angle given the trigonometric functions of the full angle.
Calculating Exact Values: Step-by-Step Examples
Let's illustrate the process with some examples:
Example 1: Finding the exact value of sin 75°
We can express 75° as the sum of 30° and 45°: 75° = 30° + 45°. Using the sum identity for sine:
sin 75° = sin (30° + 45°) = sin 30° cos 45° + cos 30° sin 45°
Substituting the known values:
sin 75° = (1/2)(√2/2) + (√3/2)(√2/2) = (√2 + √6) / 4
Example 2: Finding the exact value of cos 15°
We can express 15° as the difference of 45° and 30°: 15° = 45° - 30°. Using the difference identity for cosine:
cos 15° = cos (45° - 30°) = cos 45° cos 30° + sin 45° sin 30°
Substituting the known values:
cos 15° = (√2/2)(√3/2) + (√2/2)(1/2) = (√6 + √2) / 4
Example 3: Finding the exact value of tan 105°
We can express 105° as the sum of 60° and 45°: 105° = 60° + 45°. Using the sum identity for tangent:
tan 105° = tan (60° + 45°) = (tan 60° + tan 45°) / (1 - tan 60° tan 45°)
Substituting the known values:
tan 105° = (√3 + 1) / (1 - √3) = -2 - √3
Limitations of Calculators and the Importance of Exact Values
While calculators are invaluable tools, they only provide approximate decimal values. These approximations can lead to inaccuracies in calculations, especially when dealing with more complex trigonometric expressions or when successive approximations are involved.
Using exact values, however, ensures precision. This is especially crucial in areas like:
-
Calculus: Many calculus problems require exact values for accurate differentiation and integration.
-
Trigonometry Proofs: Using approximations can make proving trigonometric identities challenging or impossible.
-
Engineering and Physics: Accuracy in calculations is paramount in these fields, and exact values minimize error propagation.
Conclusion: Mastering Exact Values for Enhanced Mathematical Proficiency
Calculating exact values of trigonometric functions is a fundamental skill that enhances mathematical proficiency. The unit circle, special triangles, and trigonometric identities provide the tools to achieve this. While calculators offer convenience, understanding the principles behind calculating exact values is essential for accuracy, precision, and a deeper understanding of trigonometry and related mathematical concepts. By mastering these methods, you can enhance your problem-solving abilities and tackle more complex mathematical challenges with confidence. The investment in learning these techniques will significantly improve your overall mathematical understanding and capabilities.
Latest Posts
Latest Posts
-
What Is 9 5 Inches In Cm
Apr 02, 2025
-
How Much Is 155 Cm In Feet
Apr 02, 2025
-
How Many Lbs In 250 Grams
Apr 02, 2025
-
124 Cm Is How Many Inches
Apr 02, 2025
-
How Many Pounds In 350 Grams
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Exact Values Of Trig Functions Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
