Derivative Of Sqrt 2 X 2
Greels
Mar 29, 2025 · 4 min read
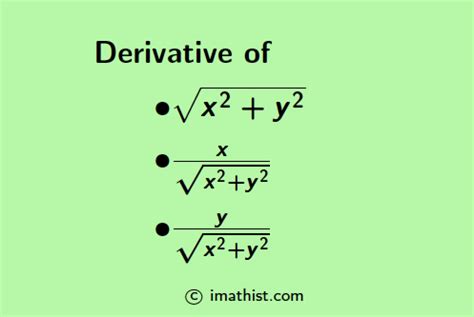
Table of Contents
Understanding the Derivative of √(2x²): A Comprehensive Guide
The derivative of a function describes its instantaneous rate of change at any given point. Understanding how to find the derivative, particularly for functions involving square roots, is crucial in calculus and various applications in science and engineering. This article delves into the detailed calculation and understanding of the derivative of √(2x²), exploring different approaches and providing a comprehensive explanation.
Understanding the Function: √(2x²)
Before diving into the derivative, let's analyze the function itself: f(x) = √(2x²). This represents a square root function with a coefficient and a squared variable inside. It's important to note the domain of this function. Since we're dealing with a square root, the expression inside the square root (2x²) must be non-negative. This means 2x² ≥ 0, which is true for all real numbers x. Therefore, the domain of f(x) is all real numbers, (-∞, ∞). However, the range is [0, ∞) because the square root of a non-negative number is always non-negative.
Method 1: Using the Power Rule and Chain Rule
The most straightforward approach to finding the derivative involves applying the power rule and the chain rule. Let's break it down:
1. Rewriting the Function
First, rewrite the function using exponents:
f(x) = √(2x²) = (2x²)<sup>1/2</sup>
This makes it easier to apply the power rule.
2. Applying the Chain Rule
The chain rule states that the derivative of a composite function is the derivative of the outer function (with the inside function left alone) times the derivative of the inside function. In this case, our outer function is u<sup>1/2</sup> and our inner function is 2x².
Let u = 2x². Then f(x) = u<sup>1/2</sup>.
3. Applying the Power Rule
The power rule states that the derivative of x<sup>n</sup> is nx<sup>n-1</sup>. Applying this to our outer function:
d(u<sup>1/2</sup>)/du = (1/2)u<sup>(1/2)-1</sup> = (1/2)u<sup>-1/2</sup> = 1/(2√u)
4. Finding the Derivative of the Inner Function
Now, we find the derivative of the inner function:
du/dx = d(2x²)/dx = 4x
5. Combining the Results
Finally, we combine the results using the chain rule:
df/dx = [d(u<sup>1/2</sup>)/du] * [du/dx] = [1/(2√u)] * [4x] = 4x / (2√(2x²)) = 2x / √(2x²)
6. Simplifying the Derivative
We can simplify this further by factoring out a √2:
df/dx = 2x / (√2 * √x²) = 2x / (√2 * |x|) = x / (|x|√(1/2)) = x / (|x|/√2) = √2 * x / |x|
Important Note: The absolute value of x, |x|, appears in the simplified derivative because √x² = |x| and not simply x. This is crucial because the original function, f(x), is always non-negative, but its derivative is not.
Therefore, the derivative of √(2x²) is √2 * x / |x|. This derivative is defined for all x except x=0.
Method 2: Implicit Differentiation
Another approach involves implicit differentiation. While it might seem more complex for this specific function, understanding this method is valuable for more intricate problems.
Let y = √(2x²). Square both sides to eliminate the square root:
y² = 2x²
Now, differentiate both sides with respect to x:
2y(dy/dx) = 4x
Solve for dy/dx:
dy/dx = 4x / (2y) = 2x / y
Substitute y = √(2x²) back into the equation:
dy/dx = 2x / √(2x²)
This leads to the same simplified result as before:
dy/dx = √2 * x / |x|
Analyzing the Derivative
The derivative, √2 * x / |x|, provides insights into the function's behavior:
- For x > 0: The derivative simplifies to √2, indicating a constant positive slope. The function is increasing.
- For x < 0: The derivative simplifies to -√2, indicating a constant negative slope. The function is decreasing.
- At x = 0: The derivative is undefined, reflecting a sharp turn or cusp in the graph at this point.
Applications of the Derivative
The derivative of √(2x²) finds applications in various fields:
- Optimization problems: Finding maxima or minima of related functions.
- Physics: Calculating instantaneous rates of change in quantities such as velocity or acceleration.
- Engineering: Analyzing curves and shapes in designing structures or systems.
- Economics: Modelling marginal costs or revenues.
Conclusion
Finding the derivative of √(2x²) requires applying the chain rule and power rule or implicit differentiation. The resultant derivative, √2 * x / |x|, reveals crucial information about the function's behavior: its increasing and decreasing intervals, and the point of non-differentiability. Understanding this process is vital for anyone working with calculus and its real-world applications. The importance of the absolute value in the final answer should not be overlooked; it's a critical element ensuring the derivative aligns with the behaviour of the original function. Mastering these techniques equips you with valuable tools for tackling more complex derivative problems in the future.
Latest Posts
Latest Posts
-
What Is 35 Inches In Centimeters
Mar 31, 2025
-
51 Inches Is What In Feet
Mar 31, 2025
-
How Many Feet Are In 96
Mar 31, 2025
-
What Is 6 Percent Of 30
Mar 31, 2025
-
How Many Inches Is 92 Mm
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of Sqrt 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
