Convert Equation To Polar Form Calculator
Greels
Apr 05, 2025 · 5 min read
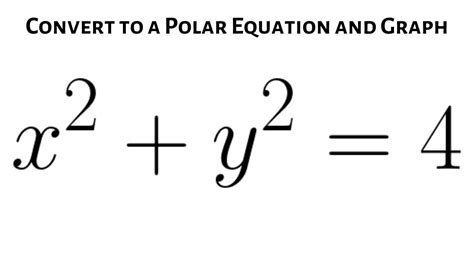
Table of Contents
Convert Equation to Polar Form Calculator: A Comprehensive Guide
Converting equations from rectangular (Cartesian) coordinates to polar coordinates is a fundamental concept in mathematics, particularly useful in fields like calculus, physics, and engineering. While the conversion process involves straightforward formulas, the calculations can become cumbersome, especially for complex equations. This is where a "convert equation to polar form calculator" becomes invaluable. This article will delve into the process of converting equations, exploring the underlying mathematics, providing practical examples, and highlighting the benefits of using a calculator for this task. We'll also discuss different types of equations and the nuances of their conversion.
Understanding Rectangular and Polar Coordinate Systems
Before we dive into the conversion process, let's briefly review the two coordinate systems involved:
Rectangular Coordinates (Cartesian): This is the familiar system where points are represented by their horizontal (x) and vertical (y) distances from the origin (0, 0).
Polar Coordinates: In this system, points are defined by their distance (r) from the origin and the angle (θ) they make with the positive x-axis. The angle θ is typically measured in radians or degrees.
The relationship between the two systems is defined by the following equations:
- x = r cos θ
- y = r sin θ
- r² = x² + y²
- tan θ = y / x (Note: this equation only gives the principal value of θ; you need to consider the quadrant to determine the correct angle.)
The Conversion Process: From Rectangular to Polar
Converting an equation from rectangular to polar form involves substituting the rectangular coordinates (x and y) with their polar equivalents (r and θ). The process usually involves some algebraic manipulation to isolate 'r' or 'θ' or express the equation solely in terms of 'r' and 'θ'.
Let's illustrate this with a few examples:
Example 1: Converting a Simple Linear Equation
Let's convert the linear equation x + y = 1 to polar form.
-
Substitute: Replace x with r cos θ and y with r sin θ: r cos θ + r sin θ = 1
-
Solve for r: Factor out 'r': r (cos θ + sin θ) = 1
-
Final Polar Form: r = 1 / (cos θ + sin θ)
Example 2: Converting a Circle Equation
Consider the equation of a circle centered at the origin with radius 'a': x² + y² = a²
-
Substitute: Using r² = x² + y², we directly substitute: r² = a²
-
Solve for r: Taking the square root of both sides (considering both positive and negative solutions for r representing all points on the circle): r = ±a
Example 3: Converting a Parabola Equation
Converting a parabola equation, such as y = x², requires more steps:
-
Substitute: Replace x with r cos θ and y with r sin θ: r sin θ = (r cos θ)²
-
Simplify: r sin θ = r² cos² θ
-
Solve for r: Divide both sides by r (assuming r ≠ 0, which excludes the origin): sin θ = r cos² θ
-
Final Polar Form: r = sin θ / cos² θ = tan θ sec θ
The Role of a Convert Equation to Polar Form Calculator
As the complexity of the equation increases, the algebraic manipulations required for conversion become significantly more challenging. This is where a dedicated "convert equation to polar form calculator" proves invaluable. These calculators automate the substitution and simplification processes, providing a quick and accurate conversion. The advantages include:
-
Speed and Efficiency: Calculators drastically reduce the time spent on manual calculations, allowing you to focus on understanding the results and their applications.
-
Accuracy: Manual calculations are prone to errors, especially with complex equations. Calculators minimize the risk of these errors, ensuring reliable results.
-
Ease of Use: Even for users with limited mathematical experience, these calculators provide a user-friendly interface for inputting equations and obtaining polar form equivalents.
-
Handling Complex Equations: Calculators can handle equations involving trigonometric functions, exponentials, logarithms, and other complex mathematical expressions, significantly expanding the range of problems that can be tackled.
Different Types of Equations and Conversion Nuances
Different types of equations present unique challenges during the conversion process. For instance:
-
Conic Sections: Equations representing ellipses, hyperbolas, and parabolas often require careful manipulation to express them in polar form. The resulting equations may involve trigonometric functions and parameters reflecting the conic's characteristics (e.g., eccentricity, focus, etc.).
-
Implicit Equations: Equations where x and y are not explicitly expressed as functions of each other (e.g., x² + xy + y² = 1) require more sophisticated algebraic techniques for conversion, making a calculator particularly helpful.
-
Equations with Trigonometric Functions: Equations already involving trigonometric functions in rectangular form will yield more intricate polar forms, often requiring trigonometric identities for simplification.
Beyond the Basics: Applications and Further Exploration
The conversion of equations to polar form is not merely an abstract mathematical exercise. It has several practical applications:
-
Calculus: Polar coordinates are frequently used in calculus to simplify the calculation of areas, volumes, and integrals, particularly for regions with circular or radial symmetry.
-
Physics and Engineering: Polar coordinates are essential in describing phenomena with rotational symmetry, such as planetary motion, fluid dynamics, and electromagnetic fields.
-
Computer Graphics: Polar coordinates are fundamental in computer graphics for generating and manipulating circular and radial shapes.
-
Signal Processing: Polar representation can simplify the analysis of signals in the frequency domain.
Conclusion: Mastering Equation Conversions with Calculators
Converting equations from rectangular to polar form is a crucial skill in many scientific and technical disciplines. While the underlying mathematics is straightforward, the practical application can become complex. A "convert equation to polar form calculator" acts as a powerful tool, enhancing efficiency, accuracy, and allowing for the seamless exploration of more complex mathematical problems. By understanding the basic conversion process and leveraging the capabilities of these calculators, you can efficiently navigate the world of coordinate systems and unlock a deeper understanding of mathematical relationships. Remember to always check your results and ensure that they align with your understanding of the original equation's geometry and properties. Furthermore, exploring the limitations of such calculators and understanding their underlying algorithms will enable you to utilize them more effectively and interpret the results with greater confidence.
Latest Posts
Latest Posts
-
Cuanto Es 7 5 Pulgadas En Centimetros
Apr 06, 2025
-
How Many Kg Is 235 Lbs
Apr 06, 2025
-
Solve For A 7a 2b 5a B
Apr 06, 2025
-
89 Mm Is How Many Inches
Apr 06, 2025
-
190 Km Per Hour In Miles
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Convert Equation To Polar Form Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
