Approximate The Area Under The Curve Calculator
Greels
Apr 05, 2025 · 7 min read
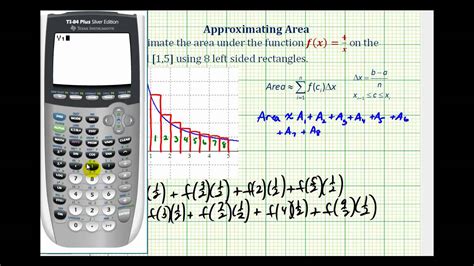
Table of Contents
Approximate the Area Under the Curve Calculator: A Comprehensive Guide
Approximating the area under a curve is a fundamental concept in calculus with wide-ranging applications in various fields, from physics and engineering to economics and statistics. While precise calculation often requires integration, numerous methods exist to approximate this area, particularly when dealing with complex functions or when an analytical solution is unavailable. This article delves into the concept, explores different approximation techniques, and highlights the utility of online "approximate the area under the curve calculator" tools.
Understanding the Area Under the Curve
The area under a curve, more formally known as the definite integral, represents the accumulation of a function's values over a specified interval. Geometrically, it's the area bounded by the curve, the x-axis, and two vertical lines corresponding to the interval's limits. Imagine calculating the distance traveled by a car given its velocity over time; the area under the velocity-time curve represents the total distance covered.
This seemingly simple concept has profound implications. For instance, in physics, the area under a force-displacement curve gives the work done, while in economics, the area under a demand curve represents the consumer surplus. The ability to efficiently and accurately approximate this area is thus crucial in numerous practical scenarios.
Methods for Approximating the Area Under the Curve
Several methods exist for approximating the area under a curve, each offering varying levels of accuracy and computational complexity. These methods are frequently implemented within "approximate the area under the curve calculator" tools. Let's explore some key techniques:
1. Rectangle Rule (Riemann Sums)
This is the most intuitive method. It involves dividing the interval into a series of rectangles, with their heights determined by the function's value at a point within each sub-interval. The area is then approximated by summing the areas of these rectangles.
- Left Riemann Sum: The height of each rectangle is determined by the function's value at the left endpoint of the sub-interval.
- Right Riemann Sum: The height is determined by the function's value at the right endpoint.
- Midpoint Rule: The height is determined by the function's value at the midpoint of the sub-interval.
The accuracy of the rectangle rule improves as the number of rectangles (and consequently, the width of each rectangle) increases. This convergence towards the true area is a fundamental principle of integral calculus. However, even with a large number of rectangles, the approximation might still be imperfect, especially for rapidly changing functions.
2. Trapezoidal Rule
The trapezoidal rule refines the rectangle rule by using trapezoids instead of rectangles. Each trapezoid is formed by connecting adjacent points on the curve with a straight line. The area of a trapezoid is easier to compute than an irregular area under a curve, making this a more efficient method. This method tends to provide a more accurate approximation than the rectangle rule, especially for smoothly varying functions. The formula for the trapezoidal rule involves averaging the left and right Riemann sums.
3. Simpson's Rule
Simpson's rule is a more sophisticated technique that approximates the curve using parabolic segments instead of straight lines (as in the trapezoidal rule). This method is particularly effective for functions that exhibit smooth curvature. It provides a significantly more accurate approximation than both the rectangle and trapezoidal rules for the same number of sub-intervals. Simpson's rule is based on approximating the function with quadratic polynomials over pairs of sub-intervals.
4. Monte Carlo Integration
This probabilistic method uses random sampling to estimate the area. Points are randomly generated within a bounding region encompassing the area under the curve. The ratio of points falling under the curve to the total number of points generated provides an estimate of the area. The accuracy of Monte Carlo integration improves with the number of random samples. While less efficient than other methods for smooth functions, it's exceptionally useful for high-dimensional integrals and complex functions where other techniques struggle.
Choosing the Right Approximation Method
The choice of approximation method depends on several factors:
- Accuracy Requirements: If high accuracy is crucial, Simpson's rule or a more advanced technique might be preferred. For less stringent requirements, the trapezoidal or even rectangle rule might suffice.
- Computational Cost: The computational cost increases with the complexity of the method and the number of sub-intervals. The rectangle rule is computationally inexpensive, while Simpson's rule or Monte Carlo integration can be more computationally intensive.
- Function Complexity: For smooth, well-behaved functions, Simpson's rule often works well. For highly oscillatory or discontinuous functions, Monte Carlo integration might be more robust.
The Role of "Approximate the Area Under the Curve Calculator" Tools
Online calculators significantly simplify the process of approximating the area under a curve. These tools automate the chosen numerical integration technique, allowing users to input the function, the interval limits, and the desired number of sub-intervals (or other relevant parameters depending on the method). The calculator then performs the calculations and presents the approximated area, often along with visualizations to aid understanding.
These calculators offer several advantages:
- Ease of Use: They eliminate the tedious manual calculations required for applying the approximation techniques.
- Time Savings: They significantly reduce the time required to obtain an approximation.
- Accessibility: They make powerful numerical integration techniques accessible to a wider audience, regardless of their mathematical expertise.
- Visualizations: Many calculators provide graphical representations of the curve and the approximation, enhancing comprehension.
However, users should be mindful of the limitations:
- Method Selection: The choice of the underlying numerical integration method can impact the accuracy of the result. Understanding the strengths and weaknesses of different methods is crucial for selecting an appropriate tool.
- Accuracy Limits: Even the most sophisticated calculators provide only approximations; the true area can only be determined through exact integration, if possible.
- Input Errors: Incorrectly inputting the function or interval limits will lead to inaccurate results.
Applications of Area Under the Curve Approximation
The ability to approximate the area under a curve has far-reaching applications across diverse disciplines:
- Physics: Calculating work done by a variable force, determining the distance traveled given a velocity-time graph, and analyzing various physical phenomena.
- Engineering: Estimating the volume of irregularly shaped objects, analyzing stress and strain in materials, and designing structures.
- Economics: Calculating consumer and producer surplus, analyzing market demand and supply, and modeling economic growth.
- Statistics: Approximating probabilities and expectations based on probability density functions, performing statistical analyses, and modeling data distributions.
- Computer Science: In image processing for analyzing shapes and textures, in machine learning algorithms for various estimations.
- Biology: Modeling population growth, analyzing growth curves, and other biological phenomena.
Advanced Techniques and Considerations
Beyond the methods discussed above, several more advanced techniques exist for approximating the area under a curve:
- Adaptive Quadrature: These methods intelligently adjust the number of sub-intervals based on the function's behavior, focusing more computational resources on regions where the function is rapidly changing.
- Gaussian Quadrature: This technique uses strategically chosen points and weights to achieve remarkably high accuracy with relatively few function evaluations.
- Romberg Integration: This method combines the trapezoidal rule with Richardson extrapolation to improve accuracy.
The choice of the "best" method often depends on the specific problem's intricacies and the desired level of accuracy. For complex functions or those with singularities, specialized techniques may be necessary.
Conclusion
Approximating the area under a curve is a powerful tool with vast applications across numerous fields. While precise calculation often requires integration, various approximation methods provide accurate estimations, particularly when dealing with complex functions or situations where analytical solutions are unavailable. "Approximate the area under the curve calculator" tools greatly simplify the process, providing convenient and accessible methods for obtaining these approximations. Understanding the underlying principles of these methods and their respective strengths and weaknesses allows for informed decision-making, ultimately leading to accurate and reliable results. Choosing the right technique, considering accuracy requirements, and using reliable tools ensures successful and efficient approximation of the area under any given curve.
Latest Posts
Latest Posts
-
What Is 42 Mm In Inches
Apr 06, 2025
-
How Many Inches Is 195 Mm
Apr 06, 2025
-
36 Feet Is How Many Meters
Apr 06, 2025
-
What Is 145 Lb In Kilograms
Apr 06, 2025
-
Cuanto Son 145 Libras En Kilos
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Approximate The Area Under The Curve Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
