9x + 8x - 12 + 7
Greels
Apr 23, 2025 · 4 min read
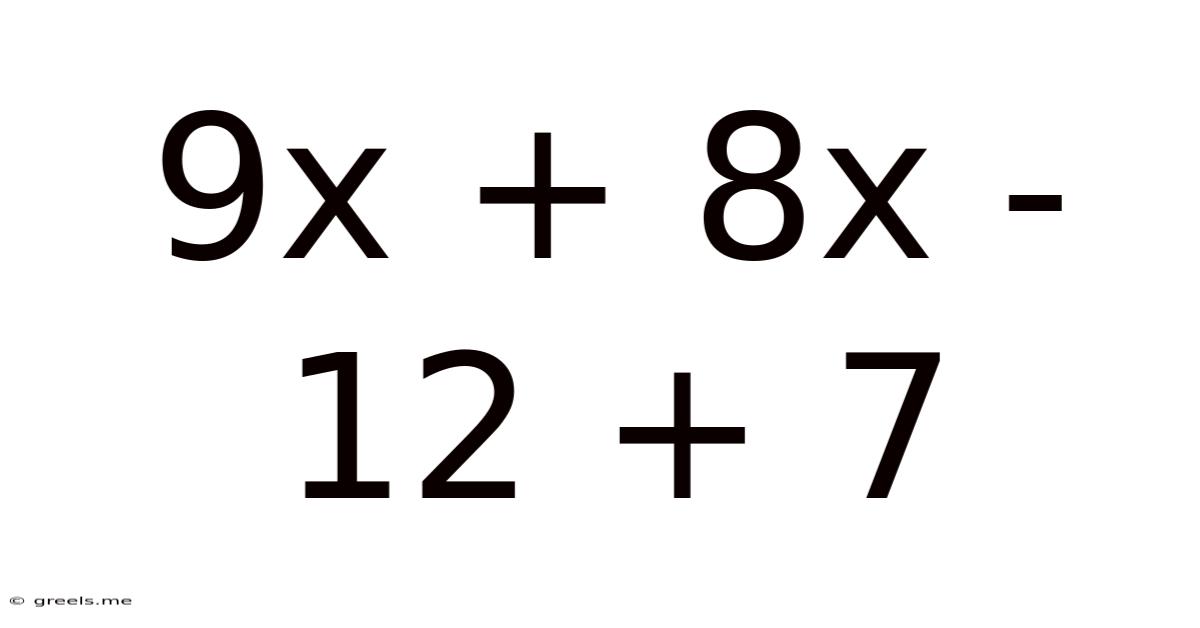
Table of Contents
Solving the Algebraic Expression: 9x + 8x - 12 + 7
This article delves into the seemingly simple algebraic expression: 9x + 8x - 12 + 7. While the expression itself might appear basic, it provides a valuable foundation for understanding fundamental algebraic principles, including combining like terms and simplifying expressions. We'll explore the step-by-step solution, discuss the underlying concepts, and even touch upon more advanced applications of similar expressions.
Understanding the Components
Before diving into the solution, let's break down the expression's components:
- 9x: This term represents 9 multiplied by the variable 'x'. The 'x' is an unknown value or a variable.
- 8x: Similar to the previous term, this signifies 8 multiplied by 'x'.
- -12: This is a constant term, a numerical value without a variable.
- +7: Another constant term.
Simplifying the Expression: A Step-by-Step Guide
The key to simplifying this expression lies in combining like terms. Like terms are terms that have the same variables raised to the same powers. In this case, our like terms are 9x and 8x, and -12 and +7.
Step 1: Combine the 'x' terms:
9x + 8x = 17x
This step involves adding the coefficients (the numbers multiplying 'x') together. Think of it like adding 9 apples and 8 apples – you get 17 apples.
Step 2: Combine the constant terms:
-12 + 7 = -5
This step involves adding the constant terms. Subtracting 12 from 7 results in -5.
Step 3: Combine the simplified terms:
17x + (-5) = 17x - 5
This is the simplified form of the original expression. We've combined the like terms to obtain a more concise representation.
The Final Simplified Expression: 17x - 5
Therefore, the solution to the algebraic expression 9x + 8x - 12 + 7 is 17x - 5. This is the simplest form of the expression, as we cannot further simplify it without knowing the value of 'x'.
Deeper Dive into Algebraic Concepts
This seemingly simple exercise showcases several core algebraic principles:
1. Combining Like Terms: The Foundation of Simplification
Combining like terms is a crucial skill in algebra. It allows us to simplify complex expressions into more manageable forms, making further calculations and analysis easier. The ability to identify and combine like terms is fundamental for solving equations and tackling more advanced algebraic problems.
2. The Importance of Order of Operations (PEMDAS/BODMAS)
While this particular expression doesn't require the strict application of the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction – PEMDAS/BODMAS), it's crucial to understand its importance in more complex algebraic problems. Knowing the correct order in which to perform operations prevents errors and ensures accurate results. In this case, we simply combined like terms, which implicitly follows the order of operations.
3. Variables and Constants: The Building Blocks of Algebra
Understanding the difference between variables (like 'x') and constants (like -12 and 7) is vital. Variables represent unknown quantities, while constants are fixed numerical values. The ability to distinguish between these two types of terms is essential for correctly manipulating algebraic expressions.
4. Coefficients: The Multipliers of Variables
Coefficients are the numerical factors that multiply variables. In our expression, 9 and 8 are the coefficients of 'x'. Understanding coefficients helps in performing operations involving variables correctly.
Applications and Extensions
The principles illustrated by this simple expression have wide-ranging applications in various fields:
-
Physics: Many physics equations involve variables and constants, often requiring simplification similar to the steps we've outlined. For example, equations for motion, forces, and energy frequently involve combining like terms.
-
Engineering: Engineers use algebraic expressions extensively in designing structures, circuits, and systems. Simplifying expressions helps in optimizing designs and ensuring efficiency.
-
Computer Science: Programming often involves manipulating variables and performing calculations, making a solid understanding of algebra essential for writing efficient and correct code.
-
Finance: Financial modeling and analysis heavily rely on algebraic expressions to represent various financial variables and relationships.
-
Economics: Economic models frequently use algebraic equations to represent economic relationships and predict future trends.
Expanding on the Concept: Solving for 'x'
While we've simplified the expression, we can take it a step further. If the simplified expression (17x - 5) were equal to a certain value, we could then solve for 'x'. For instance:
17x - 5 = 25
To solve for 'x', we would follow these steps:
Step 1: Add 5 to both sides:
17x - 5 + 5 = 25 + 5
17x = 30
Step 2: Divide both sides by 17:
17x / 17 = 30 / 17
x = 30/17 or approximately 1.76
This demonstrates how simplifying an expression is a crucial first step in solving algebraic equations.
Conclusion: Mastering the Fundamentals
The algebraic expression 9x + 8x - 12 + 7, though seemingly simple, offers a valuable opportunity to reinforce fundamental algebraic concepts. Understanding how to combine like terms, the importance of the order of operations, and the distinction between variables and constants lays a solid foundation for tackling more complex algebraic problems. The ability to simplify expressions is a crucial skill applicable across numerous fields, highlighting the practical relevance of even the most basic algebraic principles. By mastering these fundamentals, you unlock the door to a deeper understanding of mathematics and its widespread applications in the real world.
Latest Posts
Related Post
Thank you for visiting our website which covers about 9x + 8x - 12 + 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.