5x 4y 12 In Slope Intercept Form
Greels
May 02, 2025 · 4 min read
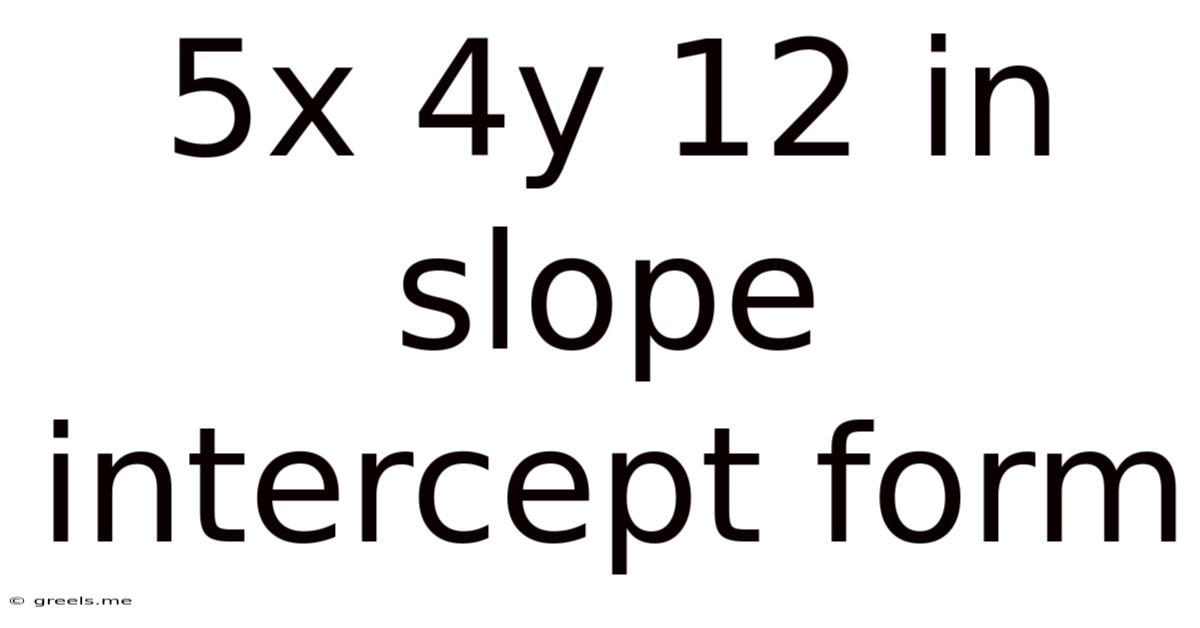
Table of Contents
Converting 5x + 4y = 12 to Slope-Intercept Form: A Comprehensive Guide
The equation 5x + 4y = 12 represents a linear relationship between two variables, x and y. While useful in its current form, converting it to slope-intercept form (y = mx + b) offers significant advantages in understanding and interpreting the line's characteristics. This form clearly reveals the slope (m) and the y-intercept (b), providing valuable insights into the line's steepness and its point of intersection with the y-axis. This guide will walk you through the process of converting 5x + 4y = 12 to slope-intercept form, explaining each step in detail and exploring the broader implications of this transformation.
Understanding Slope-Intercept Form (y = mx + b)
Before diving into the conversion, let's solidify our understanding of the slope-intercept form, y = mx + b. This equation represents a straight line where:
-
m represents the slope of the line. The slope describes the steepness of the line and is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. A slope of zero represents a horizontal line.
-
b represents the y-intercept. This is the y-coordinate of the point where the line intersects the y-axis (where x = 0). It essentially tells us where the line crosses the vertical axis.
Converting 5x + 4y = 12 to Slope-Intercept Form
The goal is to isolate 'y' on one side of the equation, leaving the equation in the form y = mx + b. Here's a step-by-step guide:
Step 1: Subtract 5x from both sides of the equation.
This step aims to move the term containing 'x' to the right side of the equation. Subtracting 5x from both sides gives us:
4y = -5x + 12
Step 2: Divide both sides of the equation by 4.
This step isolates 'y', achieving our goal of expressing the equation in slope-intercept form. Dividing both sides by 4 yields:
y = (-5/4)x + 3
Step 3: Identify the slope (m) and y-intercept (b).
Now that the equation is in the form y = mx + b, we can easily identify the slope and y-intercept:
-
Slope (m) = -5/4: This indicates a negative slope, meaning the line slopes downwards from left to right. The slope's magnitude (5/4 or 1.25) indicates the steepness of the decline. For every 4 units moved horizontally to the right, the line moves 5 units downwards.
-
Y-intercept (b) = 3: This tells us that the line intersects the y-axis at the point (0, 3).
Graphical Representation and Interpretation
The slope-intercept form allows for easy graphical representation. We know the line passes through the point (0, 3). Using the slope, we can find another point. Since the slope is -5/4, we can move 4 units to the right and 5 units down from (0,3) to find another point on the line: (4, -2). Plotting these two points and drawing a straight line through them gives us the graphical representation of the equation.
Applications and Significance of Slope-Intercept Form
Converting to slope-intercept form offers several significant advantages:
-
Easy visualization: The slope and y-intercept provide a clear picture of the line's characteristics, enabling quick and easy plotting on a graph.
-
Simple interpretation: Understanding the slope and y-intercept provides valuable insights into the relationship between the variables x and y. For example, in a real-world scenario, the slope might represent the rate of change, while the y-intercept might represent an initial value.
-
Predictive capabilities: Once the equation is in slope-intercept form, you can easily predict the value of y for any given value of x, and vice-versa.
-
Comparison with other lines: The slope-intercept form facilitates easy comparison between different lines. Lines with the same slope are parallel; lines with slopes that are negative reciprocals of each other are perpendicular.
Real-World Applications of Linear Equations
Linear equations, expressed in slope-intercept form, find applications in numerous fields:
-
Economics: Modeling supply and demand, predicting costs and revenue.
-
Physics: Describing motion, calculating velocity and acceleration.
-
Engineering: Designing structures, analyzing stresses and strains.
-
Computer science: Developing algorithms, modeling data.
-
Finance: Predicting investment growth, calculating interest rates.
Further Exploration of Linear Equations
Beyond the slope-intercept form, other forms exist, each with its own advantages:
-
Standard Form (Ax + By = C): This form is useful for finding x and y intercepts quickly and for certain algebraic manipulations.
-
Point-Slope Form (y - y1 = m(x - x1)): Useful when you know the slope and a point on the line.
Mastering the conversion of linear equations to slope-intercept form is a crucial skill in algebra and has broad applications across various disciplines. Understanding the slope and y-intercept provides valuable insights into the behavior and characteristics of the linear relationship, making it easier to interpret and apply in real-world contexts. This ability allows for accurate prediction, efficient problem-solving, and enhanced comprehension of underlying relationships within data. Remember to practice various examples to solidify your understanding and improve your proficiency in handling linear equations. Through consistent practice and application, you will develop a strong foundation in linear algebra and its practical applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5x 4y 12 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.