5x - 4 - 8x + 10
Greels
May 02, 2025 · 5 min read
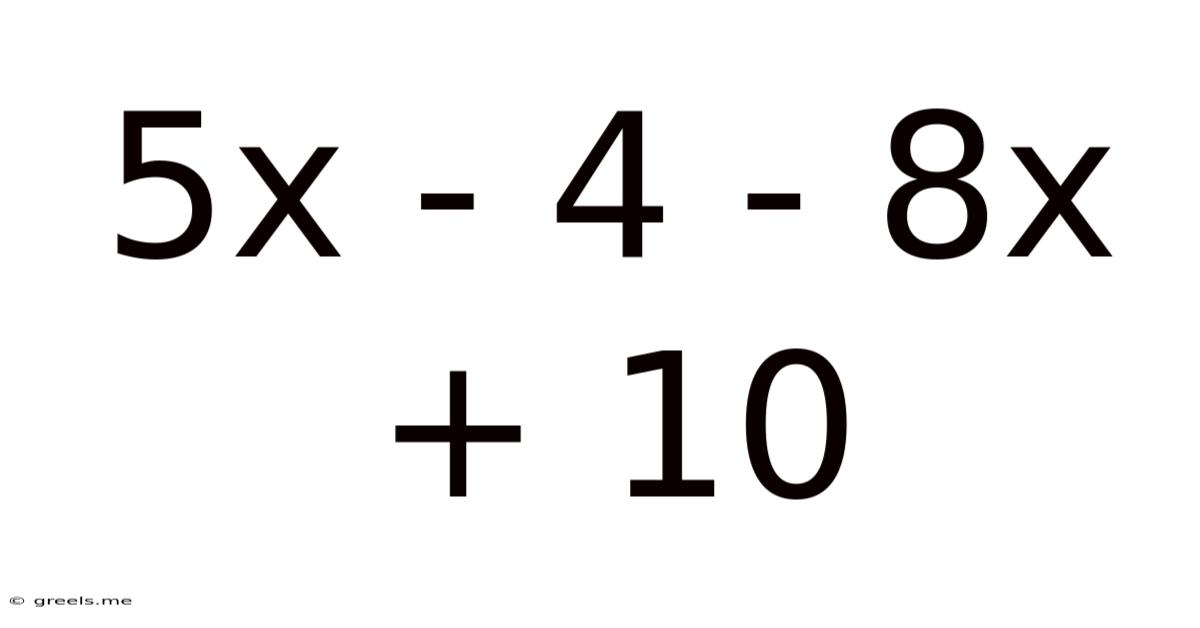
Table of Contents
Deconstructing and Solving 5x - 4 - 8x + 10: A Deep Dive into Algebraic Simplification
This article delves into the seemingly simple algebraic expression, 5x - 4 - 8x + 10, providing a comprehensive exploration of its simplification, applications, and the underlying mathematical principles. We'll move beyond a simple solution to examine the core concepts involved, making this understanding accessible to students of all levels, from beginners grasping basic algebra to those seeking a more nuanced understanding of algebraic manipulation.
H2: Understanding the Components: Variables, Constants, and Operators
Before we tackle the simplification, let's define the elements within the expression:
-
Variables: In this case, 'x' represents a variable. A variable is a symbol (usually a letter) that stands for an unknown numerical value. Its value can change depending on the context of the equation or problem.
-
Constants: '-4' and '+10' are constants. Constants are fixed numerical values that do not change.
-
Operators: '+', '-', represent operators that define the mathematical operations (addition and subtraction) to be performed on the terms.
H2: Simplifying the Expression: Combining Like Terms
The key to simplifying this algebraic expression lies in combining like terms. Like terms are terms that contain the same variables raised to the same powers. In our expression, 5x and -8x are like terms because they both contain the variable 'x' raised to the power of 1 (implicitly). Similarly, -4 and +10 are like terms because they are both constants.
H3: The Step-by-Step Process
-
Identify like terms: We've already identified our like terms: 5x and -8x; -4 and +10.
-
Combine like terms: Add or subtract the coefficients (the numbers in front of the variables) of the like terms.
-
For the 'x' terms: 5x - 8x = -3x
-
For the constant terms: -4 + 10 = +6
-
-
Rewrite the simplified expression: Combining the simplified like terms gives us the simplified expression: -3x + 6
H2: Visualizing the Simplification: A Geometric Approach
Algebraic expressions can often be visualized geometrically. While this expression doesn't directly lend itself to a simple geometric representation like area calculations, we can think of it in terms of combining lengths or quantities.
Imagine 'x' representing the length of a certain object. '5x' would then represent five times that length, and '-8x' would represent removing eight times that length. Combining these would leave you with a length represented by -3x. Similarly, the constants -4 and +10 can be visualized as adding and subtracting fixed quantities.
This visualization helps to solidify the understanding that we are not manipulating numbers randomly but are combining quantifiable entities.
H2: Solving for x: Finding the Value of the Variable
The simplified expression, -3x + 6, is not an equation. An equation has an equals sign (=), indicating that two expressions are equal. To solve for 'x', we need an equation, such as:
-3x + 6 = 0 (Example 1)
-3x + 6 = 12 (Example 2)
H3: Solving Example 1: -3x + 6 = 0
-
Isolate the term with 'x': Subtract 6 from both sides of the equation:
-3x = -6
-
Solve for 'x': Divide both sides by -3:
x = 2
Therefore, in this equation, the value of x that satisfies the equation is 2.
H3: Solving Example 2: -3x + 6 = 12
-
Isolate the term with 'x': Subtract 6 from both sides of the equation:
-3x = 6
-
Solve for 'x': Divide both sides by -3:
x = -2
In this equation, the value of x that satisfies the equation is -2. This demonstrates that the value of 'x' depends entirely on the context of the equation.
H2: Applications of Algebraic Simplification
Simplifying algebraic expressions is fundamental to numerous mathematical applications, including:
-
Solving equations: As shown above, simplifying an expression is a crucial step in solving equations for unknown variables.
-
Problem-solving: Many real-world problems can be modeled using algebraic expressions. Simplifying these expressions makes them easier to analyze and solve. Examples include calculating costs, profits, or distances.
-
Calculus: Simplification is essential in calculus for differentiating and integrating functions.
-
Physics and Engineering: Algebraic manipulation forms the bedrock of many physical and engineering calculations.
-
Computer Programming: Simplifying expressions leads to more efficient and readable code.
H2: Further Exploration: Expanding the Scope
The expression 5x - 4 - 8x + 10 is a simple example. More complex expressions involve:
-
Higher powers of x: Terms with x², x³, etc. require similar principles of combining like terms, but with careful attention to the exponents.
-
Multiple variables: Expressions with multiple variables (e.g., 2x + 3y - z) require combining like terms based on each variable.
-
Parentheses and brackets: Expressions with parentheses or brackets necessitate following the order of operations (PEMDAS/BODMAS) to correctly simplify.
-
Fractions and decimals: The principles of simplification remain the same, even when dealing with fractions and decimals.
H2: Common Mistakes to Avoid
When simplifying algebraic expressions, some common mistakes to avoid include:
-
Incorrectly combining unlike terms: Remember, only like terms can be combined.
-
Errors in arithmetic: Double-check your addition, subtraction, multiplication, and division.
-
Neglecting negative signs: Pay close attention to negative signs, as they can easily lead to mistakes.
-
Ignoring the order of operations: Follow the order of operations (PEMDAS/BODMAS) carefully, particularly when dealing with expressions involving parentheses or brackets.
H2: Practicing Your Skills: Exercises
To reinforce your understanding, try simplifying the following expressions:
-
7y + 3 - 2y - 5
-
4a² + 6a - a² - 2a
-
3(2x + 1) - 2(x - 4)
-
(5x - 2) + (3x + 7)
-
10b/5 - 2b
H2: Conclusion: Mastering the Fundamentals
The seemingly simple expression 5x - 4 - 8x + 10 serves as a powerful gateway to understanding core algebraic principles. By mastering the techniques of combining like terms and solving for variables, you lay a strong foundation for tackling more complex mathematical concepts and real-world applications. Remember to practice regularly, understand the underlying principles, and avoid the common pitfalls to develop a solid understanding of algebraic simplification. The journey of mastering algebra is iterative; consistent effort and mindful practice are key to success.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5x - 4 - 8x + 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.