5x 3y 9 In Slope Intercept Form
Greels
May 02, 2025 · 5 min read
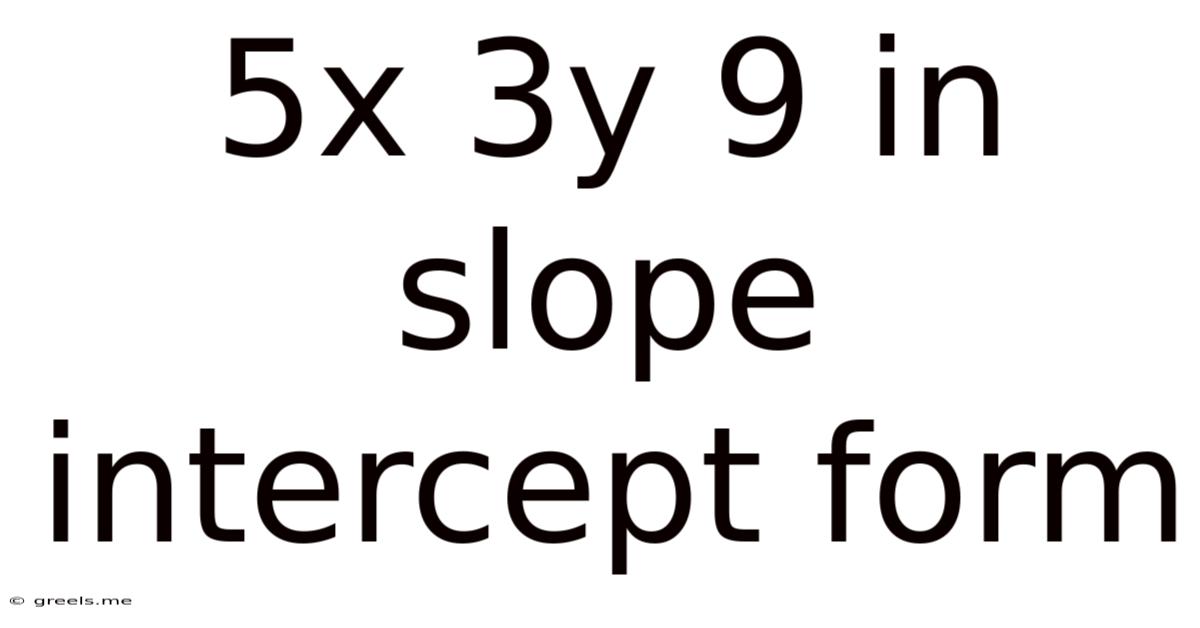
Table of Contents
Unveiling the Secrets of 5x + 3y = 9: A Deep Dive into Slope-Intercept Form
The equation 5x + 3y = 9 represents a linear relationship between two variables, x and y. While useful in its current form, transforming it into slope-intercept form (y = mx + b) unlocks a wealth of information about the line it describes, revealing its slope (m) and y-intercept (b) instantly. This transformation is a fundamental concept in algebra and has far-reaching applications in various fields, from physics and engineering to economics and finance. This comprehensive guide will not only show you how to convert 5x + 3y = 9 into slope-intercept form but also delve into the why behind the process and explore its broader implications.
Understanding Slope-Intercept Form: y = mx + b
Before we embark on the transformation, let's solidify our understanding of the slope-intercept form: y = mx + b. This seemingly simple equation holds the key to understanding the characteristics of any straight line.
- y: Represents the dependent variable – its value depends on the value of x.
- x: Represents the independent variable – its value is chosen freely.
- m: Represents the slope of the line. The slope describes the steepness and direction of the line. A positive slope indicates an upward trend (from left to right), while a negative slope indicates a downward trend. A slope of zero signifies a horizontal line. The slope is calculated as the change in y divided by the change in x (rise over run).
- b: Represents the y-intercept – the point where the line crosses the y-axis (where x = 0).
Transforming 5x + 3y = 9 into Slope-Intercept Form
Now, let's transform the given equation, 5x + 3y = 9, into the slope-intercept form. The goal is to isolate 'y' on one side of the equation.
-
Subtract 5x from both sides:
This step moves the term containing 'x' to the right side of the equation:
3y = -5x + 9
-
Divide both sides by 3:
This isolates 'y' and gives us the slope-intercept form:
y = (-5/3)x + 3
Therefore, the slope-intercept form of the equation 5x + 3y = 9 is y = (-5/3)x + 3.
Interpreting the Results: Slope and Y-Intercept
From the slope-intercept form, y = (-5/3)x + 3, we can readily extract crucial information:
-
Slope (m) = -5/3: This tells us that the line has a negative slope, meaning it slopes downwards from left to right. The value -5/3 indicates that for every 3 units increase in x, y decreases by 5 units.
-
Y-intercept (b) = 3: This means the line intersects the y-axis at the point (0, 3).
Visualizing the Line: Graphing the Equation
Plotting the line on a graph provides a visual representation of the equation. We can use the y-intercept (0, 3) as our starting point. Since the slope is -5/3, we can find another point on the line by moving 3 units to the right and 5 units down from the y-intercept, resulting in the point (3, -2). Connecting these two points gives us the graph of the line.
Key Characteristics from the Graph:
- Negative Slope: The line descends as we move from left to right, confirming the negative slope.
- Y-intercept: The line clearly intersects the y-axis at the point (0, 3).
- X-intercept: While not directly provided by the slope-intercept form, we can find the x-intercept (where y = 0) by setting y = 0 in the original equation or the slope-intercept form and solving for x. In this case, the x-intercept is (9/5, 0).
Applications of Slope-Intercept Form
The slope-intercept form is more than just a mathematical manipulation; it's a powerful tool with wide-ranging applications:
1. Predictive Modeling:
In various fields like economics and finance, linear equations can model trends and make predictions. The slope-intercept form allows for easy prediction of y values given an x value, and vice-versa.
2. Engineering and Physics:
Linear relationships often appear in physics and engineering problems, such as calculating the velocity of an object or determining the relationship between force and displacement. The slope-intercept form simplifies calculations and analysis.
3. Data Analysis:
When analyzing datasets, if the data shows a linear trend, the slope-intercept form can be used to represent the trend line and understand the relationship between the variables.
4. Computer Graphics:
In computer graphics, lines are fundamental elements. The slope-intercept form is used to define and draw lines efficiently.
5. Cost Analysis:
In business, linear equations can model cost functions. The slope represents the variable cost per unit, while the y-intercept represents fixed costs. Understanding this allows for effective cost management and pricing strategies.
Beyond the Basics: Exploring Related Concepts
Understanding the slope-intercept form opens doors to exploring several related concepts:
1. Point-Slope Form:
The point-slope form (y - y₁ = m(x - x₁)) is another way to represent a line, using the slope and a point on the line. It can be easily converted to slope-intercept form.
2. Standard Form:
The standard form (Ax + By = C) is a general way to represent a line, and as we've shown, it can be converted to slope-intercept form.
3. Parallel and Perpendicular Lines:
Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals of each other. Understanding this allows for analyzing the relationships between different lines.
4. Systems of Linear Equations:
Multiple linear equations can be solved simultaneously to find the point of intersection, which is crucial in various optimization problems.
Conclusion: Mastering the Slope-Intercept Form
The transformation of 5x + 3y = 9 into its slope-intercept form, y = (-5/3)x + 3, is not merely an algebraic exercise; it's a gateway to understanding and applying linear relationships in diverse contexts. By grasping the significance of the slope and y-intercept, we unlock a powerful tool for analysis, prediction, and problem-solving across a multitude of fields. This deep dive has provided not only the mechanics of the conversion but also the broader implications and applications of this fundamental concept in mathematics. Mastering the slope-intercept form empowers you with a valuable skillset applicable far beyond the classroom.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5x 3y 9 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.