5/6 Divided By 7/10 In Simplest Form
Greels
May 03, 2025 · 5 min read
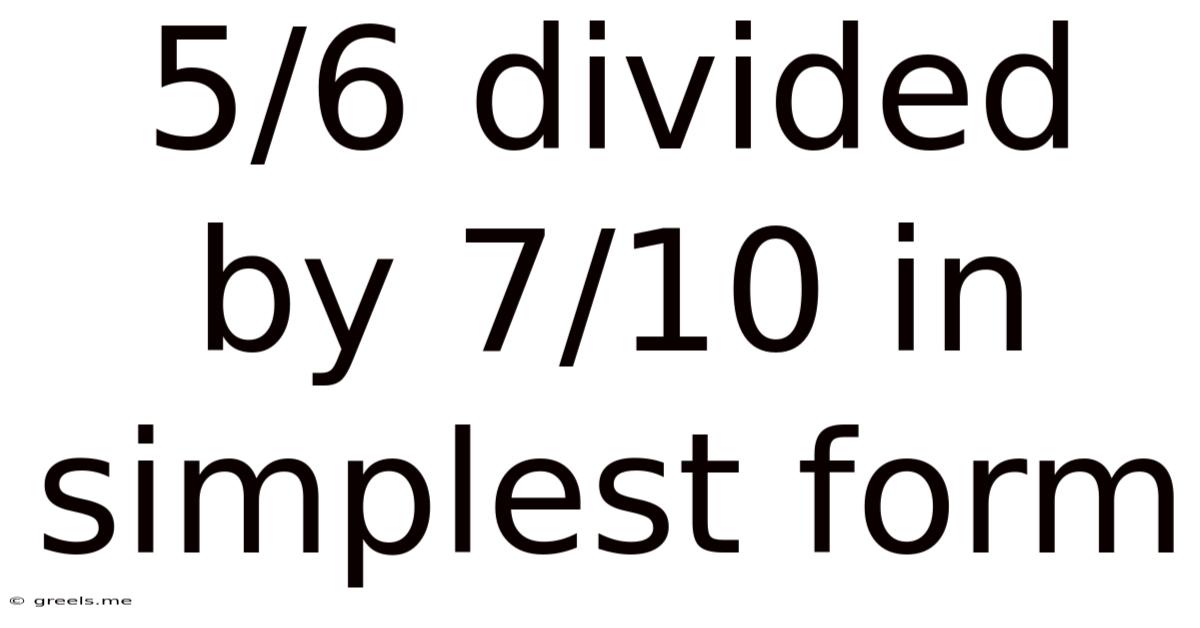
Table of Contents
5/6 Divided by 7/10 in Simplest Form: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This comprehensive guide will walk you through dividing 5/6 by 7/10, explaining each step in detail and providing valuable insights into fraction manipulation. We'll explore the concept thoroughly, ensuring you grasp not just the solution but the underlying principles. By the end, you'll be confident in tackling similar fraction division problems.
Understanding Fraction Division
Before we dive into the specific problem of 5/6 divided by 7/10, let's solidify our understanding of fraction division. The core principle is to invert the second fraction (the divisor) and then multiply. This seemingly simple rule stems from the mathematical definition of division as the inverse of multiplication.
When we divide a number (a) by another number (b), we are essentially asking, "How many times does b fit into a?" In fraction division, this translates to finding the multiplicative inverse of the divisor and then multiplying.
The multiplicative inverse, also known as the reciprocal, is simply the fraction flipped upside down. For example, the reciprocal of 7/10 is 10/7.
Therefore, the general formula for dividing fractions is:
a/b ÷ c/d = a/b × d/c
Step-by-Step Solution: 5/6 ÷ 7/10
Now, let's apply this formula to our specific problem: 5/6 ÷ 7/10.
Step 1: Invert the second fraction (the divisor).
The divisor is 7/10. Inverting it gives us 10/7.
Step 2: Change the division sign to a multiplication sign.
Our problem now becomes: 5/6 × 10/7
Step 3: Multiply the numerators (top numbers) together.
5 × 10 = 50
Step 4: Multiply the denominators (bottom numbers) together.
6 × 7 = 42
Step 5: Write the result as a single fraction.
This gives us the fraction 50/42.
Step 6: Simplify the fraction to its simplest form.
To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD of 50 and 42 is 2.
Dividing both the numerator and denominator by 2, we get:
50 ÷ 2 = 25 42 ÷ 2 = 21
Therefore, the simplest form of 50/42 is 25/21.
The Final Answer and its Implications
Therefore, 5/6 divided by 7/10, expressed in its simplest form, is 25/21. This is an improper fraction (the numerator is larger than the denominator), which can also be expressed as a mixed number.
To convert 25/21 to a mixed number, we perform the division:
25 ÷ 21 = 1 with a remainder of 4.
So, 25/21 can also be written as 1 4/21.
This result has practical implications in various fields, from cooking (adjusting recipes) to engineering (calculating dimensions) and beyond. Understanding fraction division is fundamental to solving numerous real-world problems.
Further Exploration: Different Approaches and Concepts
While the method above is the most common and straightforward approach, let's explore some related concepts to enhance your understanding of fraction division.
Understanding the Concept of "Dividing by a Fraction"
Dividing by a fraction is essentially the same as multiplying by its reciprocal. Consider the following:
If you divide a number by 1/2, you're asking "how many halves are there in that number?". This is the same as multiplying by 2. This highlights the inverse relationship between division and multiplication when dealing with fractions.
Working with Mixed Numbers
If either 5/6 or 7/10 were mixed numbers, we would first convert them into improper fractions before applying the division process. For instance, if we had 1 1/6 divided by 7/10, we'd first convert 1 1/6 to 7/6 and then proceed with the division as described earlier.
Simplifying Fractions Before Multiplying
While we simplified the fraction after multiplying in the example, it's often more efficient to simplify before multiplying. This involves canceling out common factors between the numerators and denominators.
For example, in 5/6 × 10/7, we can see that 10 and 6 share a common factor of 2. We can simplify this before multiplication:
(5/6) × (10/7) = (5/3) × (5/7) = 25/21
This method avoids dealing with larger numbers, making the calculation easier and less prone to errors.
Checking Your Work
Always check your answer. A simple way is to estimate the answer. 5/6 is approximately 1, and 7/10 is approximately 1/2. Dividing 1 by 1/2 should give you 2. Our answer, 25/21, is slightly more than 1, which is consistent with our estimate.
Practical Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous real-world applications:
- Cooking and Baking: Adjusting recipes to serve more or fewer people often requires dividing fractions.
- Sewing and Tailoring: Calculating fabric requirements for garments involves dividing fractions to determine the needed lengths and widths.
- Construction and Engineering: Calculating dimensions and material quantities in construction projects often necessitates fraction division.
- Finance and Budgeting: Dividing your budget into fractions for different expenses requires an understanding of fraction division.
- Data Analysis: In statistical analysis, data is frequently represented as fractions, making fraction division an essential skill.
Conclusion: Mastering Fraction Division
Mastering fraction division is a crucial skill for anyone who wants to confidently tackle various mathematical problems, both in academic and practical settings. By understanding the process of inverting and multiplying, and by practicing simplifying fractions, you can efficiently and accurately divide fractions. Remember to always check your work to ensure accuracy and build your confidence in this essential mathematical operation. Through consistent practice and a thorough understanding of the underlying principles, you'll be well-equipped to tackle any fraction division problem with ease and precision. The ability to perform this calculation correctly is invaluable across many disciplines and will undoubtedly serve you well in your academic and professional pursuits.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5/6 Divided By 7/10 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.