49 To The Power Of 1/2
Greels
May 03, 2025 · 6 min read
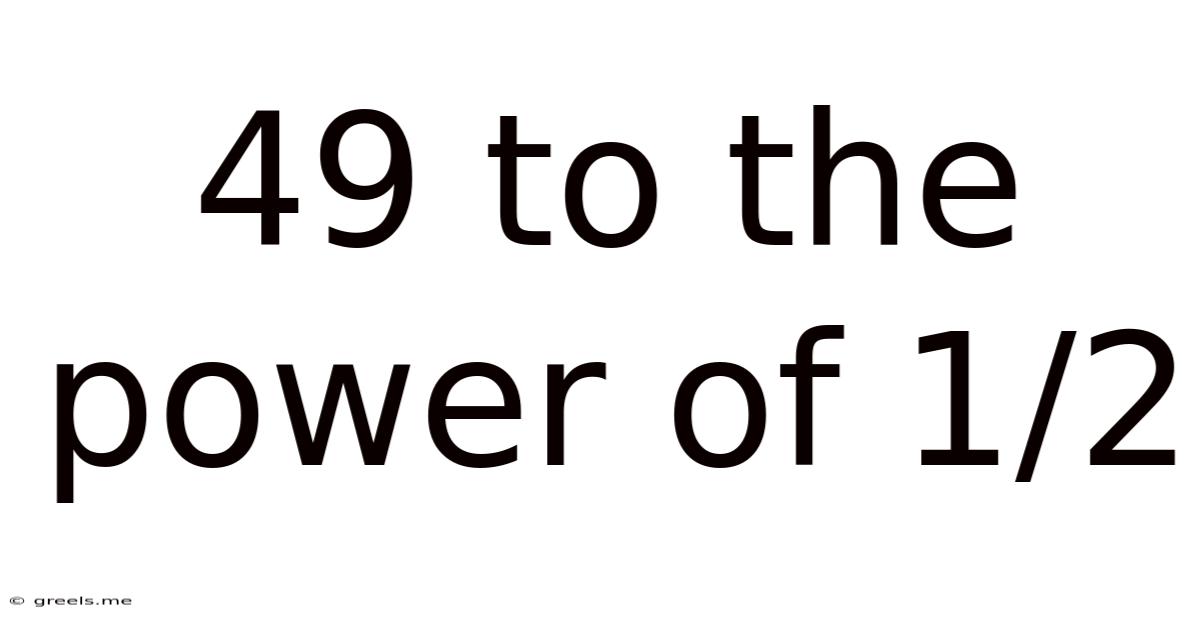
Table of Contents
49 to the Power of 1/2: Unveiling the Fundamentals of Fractional Exponents and Square Roots
The seemingly simple expression "49 to the power of 1/2" (written as 49<sup>1/2</sup>) opens a door to a fundamental concept in mathematics: fractional exponents and their close relationship to roots. Understanding this concept is crucial for anyone navigating algebra, calculus, and various scientific fields. This article will delve into the meaning of 49<sup>1/2</sup>, exploring its calculation, its implications within broader mathematical frameworks, and its practical applications.
Deciphering the Fractional Exponent: What Does 1/2 Mean?
The exponent 1/2 signifies a square root. In general terms, x<sup>1/n</sup> represents the n<sup>th</sup> root of x. Therefore, 49<sup>1/2</sup> is equivalent to the square root of 49, symbolized as √49. The square root of a number is a value that, when multiplied by itself, gives the original number.
Understanding Roots: A Deeper Dive
Before tackling 49<sup>1/2</sup> directly, let's solidify our understanding of roots. We can think of roots as the inverse operation of exponentiation. For instance:
- Squaring: 7 x 7 = 49 (7 squared, or 7²)
- Square Rooting: √49 = 7 (the number that, when multiplied by itself, equals 49)
Similarly:
- Cubing: 2 x 2 x 2 = 8 (2 cubed, or 2³)
- Cube Rooting: ∛8 = 2 (the number that, when multiplied by itself three times, equals 8)
This inverse relationship is key to understanding fractional exponents. The exponent indicates the type of root, while the numerator (in this case, 1) indicates the power to which the root is raised (which is simply itself in this instance).
Calculating 49 to the Power of 1/2
Now, let's return to our original problem: 49<sup>1/2</sup>. Since this is equivalent to √49, we are looking for a number that, when multiplied by itself, equals 49. That number is 7. Therefore:
49<sup>1/2</sup> = √49 = 7
This seemingly straightforward calculation underpins many more complex mathematical operations.
Expanding the Concept: Fractional Exponents Beyond 1/2
The concept of fractional exponents extends far beyond the simple case of 1/2 (square root). Consider the following:
- Cube root: 8<sup>1/3</sup> = ∛8 = 2
- Fourth root: 16<sup>1/4</sup> = ⁴√16 = 2
- nth root: x<sup>1/n</sup> = <sup>n</sup>√x
The general rule is that x<sup>m/n</sup> = (<sup>n</sup>√x)<sup>m</sup>. This means you take the nth root of x and then raise the result to the power of m. Let’s illustrate with an example:
- 8<sup>2/3</sup>: First, find the cube root of 8 (8<sup>1/3</sup> = 2). Then, square the result (2² = 4). Therefore, 8<sup>2/3</sup> = 4.
This demonstrates the power and versatility of fractional exponents in simplifying complex mathematical expressions.
Applications of Fractional Exponents and Square Roots
The concept of 49<sup>1/2</sup>, and fractional exponents in general, isn't just a theoretical exercise. It has numerous practical applications across various fields:
1. Geometry and Trigonometry:
Fractional exponents are fundamental in calculating areas, volumes, and other geometric properties. For example, finding the side length of a square given its area involves taking the square root (exponent of 1/2). Similarly, many trigonometric functions and their inverses rely heavily on these concepts.
2. Physics and Engineering:
In physics, square roots frequently appear in formulas related to velocity, acceleration, and energy calculations. For instance, the formula for the speed of a wave often involves square roots. In engineering, calculating the strength of materials or the stability of structures frequently uses square root calculations.
3. Statistics and Data Analysis:
Standard deviation, a crucial measure of data dispersion, involves taking the square root of the variance. This provides a crucial metric for understanding the spread of data around the mean.
4. Finance and Economics:
In financial modeling, fractional exponents appear in formulas related to compound interest, present value, and future value calculations. Understanding these calculations is essential for investment analysis and financial planning.
Connecting Fractional Exponents to Other Mathematical Concepts
Understanding 49<sup>1/2</sup> allows for a deeper appreciation of various interconnected mathematical concepts:
1. Radicals and Exponents: The Interplay
The expression 49<sup>1/2</sup> highlights the close relationship between radicals (square root symbols) and exponents. They are essentially two different notations representing the same mathematical operation. This understanding simplifies problem-solving and allows for flexibility in calculations.
2. Laws of Exponents: Extending the Rules
The rules governing integer exponents extend to fractional exponents. For example:
- Product rule: x<sup>a</sup> * x<sup>b</sup> = x<sup>a+b</sup> (holds true for fractional a and b)
- Quotient rule: x<sup>a</sup> / x<sup>b</sup> = x<sup>a-b</sup> (holds true for fractional a and b)
- Power rule: (x<sup>a</sup>)<sup>b</sup> = x<sup>ab</sup> (holds true for fractional a and b)
Mastering these rules provides a foundation for manipulating and simplifying complex expressions involving fractional exponents.
3. Complex Numbers: Beyond Real Numbers
While 49<sup>1/2</sup> yields a real number (7), fractional exponents can also result in complex numbers. For example, finding the square root of a negative number involves the imaginary unit i (where i² = -1).
Mastering 49 to the Power of 1/2 and Beyond: Practical Tips
To truly grasp the concept of 49<sup>1/2</sup> and fractional exponents, consider these tips:
- Practice Regularly: Solve numerous problems involving fractional exponents to build your understanding and intuition.
- Visualize: Use geometric representations or diagrams to aid in your understanding of roots and exponents.
- Break Down Complex Problems: Decompose complex expressions into smaller, manageable steps.
- Utilize Online Resources: Many websites and educational platforms provide interactive exercises and explanations of fractional exponents.
- Seek Clarification: Don't hesitate to seek help from teachers, tutors, or online communities if you encounter difficulties.
Conclusion: Unlocking the Power of Fractional Exponents
The seemingly simple expression 49<sup>1/2</sup> serves as a gateway to a world of mathematical possibilities. Understanding fractional exponents, their relationship to roots, and their applications across various disciplines is crucial for anyone seeking to develop a strong mathematical foundation. By mastering these concepts, you unlock the ability to tackle complex problems and further explore the fascinating realm of mathematics. The journey from understanding 49<sup>1/2</sup> can lead to a deeper appreciation of the elegance and power inherent in mathematical principles. Embrace the challenge, and you will undoubtedly reap the rewards.
Latest Posts
Related Post
Thank you for visiting our website which covers about 49 To The Power Of 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.