3y + 7 + 4y + 3
Greels
May 03, 2025 · 4 min read
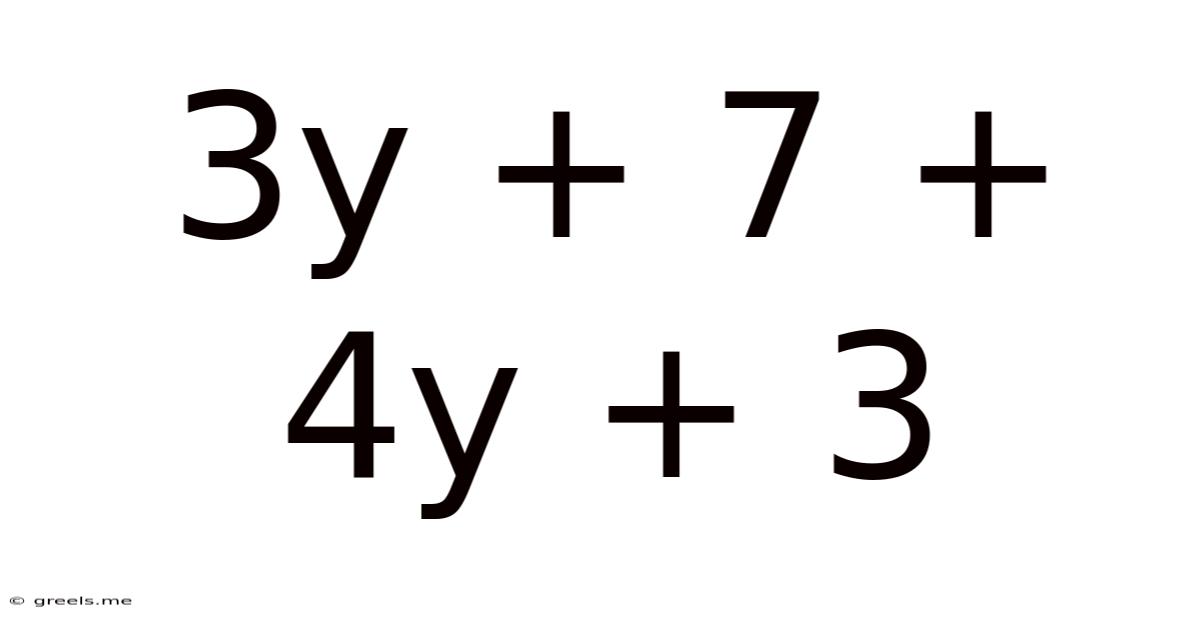
Table of Contents
Simplifying Algebraic Expressions: A Deep Dive into 3y + 7 + 4y + 3
This article provides a comprehensive guide to simplifying the algebraic expression 3y + 7 + 4y + 3. We'll explore the fundamental principles of algebra involved, delve into the step-by-step simplification process, and discuss related concepts to build a strong understanding of algebraic manipulation. This in-depth analysis aims to be useful for students learning algebra, as well as anyone looking to refresh their knowledge of fundamental mathematical concepts.
Understanding Algebraic Expressions
Before we tackle the simplification of 3y + 7 + 4y + 3, let's clarify what algebraic expressions are. An algebraic expression is a mathematical phrase that combines numbers, variables, and operators (such as +, -, ×, ÷). Variables, usually represented by letters like 'x' or 'y', represent unknown values. The expression 3y + 7 + 4y + 3 contains:
- Variables: 'y' represents an unknown numerical value.
- Constants: 7 and 3 are constants, meaning their values remain unchanged.
- Coefficients: 3 and 4 are coefficients, multiplying the variable 'y'.
- Operators: '+' indicates addition.
The goal of simplifying an algebraic expression is to write it in a more concise and manageable form without altering its value.
Simplifying 3y + 7 + 4y + 3: A Step-by-Step Approach
Simplifying 3y + 7 + 4y + 3 relies on the concept of combining like terms. Like terms are terms that have the same variable raised to the same power. In this expression, the like terms are:
- 3y and 4y: Both terms contain the variable 'y' raised to the power of 1 (implicitly, as y¹).
- 7 and 3: Both are constants.
Here's the step-by-step simplification:
Step 1: Identify Like Terms
As already mentioned, we have two sets of like terms: 3y and 4y; and 7 and 3.
Step 2: Combine Like Terms
To combine like terms, we add (or subtract) their coefficients.
- For the 'y' terms: 3y + 4y = (3 + 4)y = 7y
- For the constant terms: 7 + 3 = 10
Step 3: Write the Simplified Expression
Combining the simplified like terms, we get the simplified expression: 7y + 10
Further Exploration of Algebraic Simplification
Understanding the simplification of 3y + 7 + 4y + 3 lays the groundwork for tackling more complex algebraic expressions. Let's explore some related concepts:
The Commutative Property of Addition
The commutative property states that the order of addition doesn't affect the result. This means that 3y + 7 + 4y + 3 is equivalent to 3y + 4y + 7 + 3. Rearranging the terms to group like terms together often makes the simplification process easier.
The Associative Property of Addition
The associative property states that the grouping of terms in addition doesn't affect the result. For example, (3y + 7) + (4y + 3) is the same as 3y + (7 + 4y) + 3. While not strictly necessary for this particular simplification, understanding the associative property is crucial when dealing with more intricate expressions.
Distributive Property
The distributive property allows us to expand expressions involving parentheses. For example, if we had an expression like 2(y + 5), we would distribute the 2 to both terms inside the parentheses: 2(y + 5) = 2y + 10. While not directly applicable here, understanding the distributive property is essential for more advanced algebraic manipulations.
Solving Equations
Simplifying algebraic expressions is a crucial step in solving algebraic equations. An equation is a mathematical statement that shows the equality of two expressions. For instance, if we had the equation 3y + 7 + 4y + 3 = 20, we would first simplify the left side to 7y + 10, and then solve for 'y'. This would involve further algebraic operations like subtraction and division.
Applications of Algebraic Simplification
Algebraic simplification is a fundamental skill used extensively across various fields, including:
- Physics: Simplifying equations to solve for unknown variables such as velocity, acceleration, or force.
- Engineering: Designing structures, circuits, and systems by manipulating and solving algebraic equations.
- Computer Science: Developing algorithms and software by working with mathematical models and logical expressions.
- Finance: Calculating interest, compound interest, and other financial calculations.
- Economics: Developing economic models and forecasting trends through mathematical analysis.
Practice Problems
To solidify your understanding, try simplifying these algebraic expressions using the techniques discussed above:
- 5x + 2 + 3x + 8
- 2a - 5 + 4a + 1
- 6b + 9 - 2b - 3
- -y + 7 + 3y - 2
- 4(x + 2) + 3x
Conclusion
Simplifying the algebraic expression 3y + 7 + 4y + 3, resulting in 7y + 10, is a foundational concept in algebra. Understanding the principles of combining like terms, along with the commutative and associative properties of addition, is vital for success in algebra and various related fields. By mastering these fundamental skills, you build a strong foundation for tackling more complex mathematical problems and real-world applications. Remember to practice regularly to enhance your proficiency in simplifying algebraic expressions and solving equations. Through consistent practice and a solid grasp of the underlying principles, you'll become confident and adept at manipulating algebraic expressions efficiently and accurately.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3y + 7 + 4y + 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.