2x 3y 12 Solve For Y
Greels
Apr 23, 2025 · 5 min read
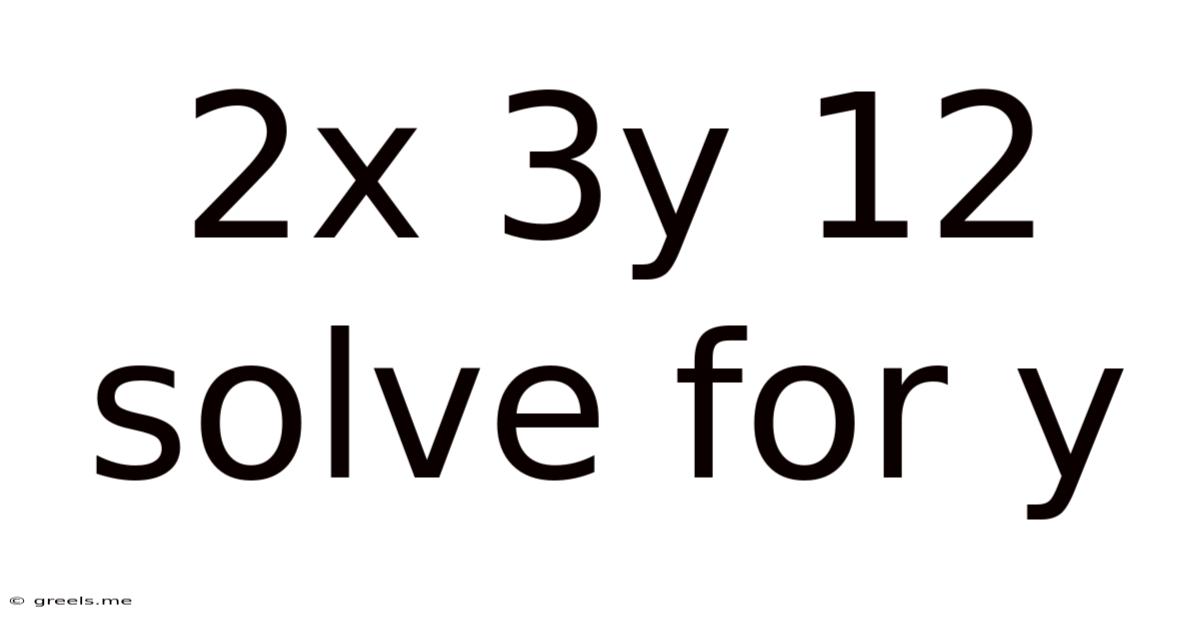
Table of Contents
Solving for 'y': A Deep Dive into 2x + 3y = 12
This article provides a comprehensive guide on how to solve the equation 2x + 3y = 12 for 'y', covering various approaches and extending the understanding to related algebraic concepts. We'll explore different methods, discuss their applications, and delve into the practical implications of solving for a specific variable within an equation. This isn't just about finding the answer; it's about understanding the process and its broader significance in mathematics.
Understanding the Equation: 2x + 3y = 12
The equation 2x + 3y = 12 represents a linear equation in two variables, 'x' and 'y'. This means that when graphed, it forms a straight line. The equation demonstrates a relationship between 'x' and 'y' where a change in one variable affects the value of the other. Solving for 'y' means isolating 'y' on one side of the equation, expressing it in terms of 'x'. This allows us to determine the value of 'y' for any given value of 'x'.
The Importance of Isolating Variables
Isolating a variable is a fundamental step in algebra. It allows us to understand the relationship between variables and predict the value of one variable based on the value of another. This is crucial in various fields, from physics and engineering to economics and computer science, where models often rely on relationships between multiple variables.
Methods to Solve for 'y'
We can solve the equation 2x + 3y = 12 for 'y' using several algebraic methods. Let's examine the most common approaches:
Method 1: Subtraction and Division
This is the most straightforward method. We aim to isolate 'y' by performing inverse operations:
-
Subtract 2x from both sides: This eliminates '2x' from the left side, leaving only the term with 'y'. The equation becomes:
3y = 12 - 2x
-
Divide both sides by 3: This isolates 'y', giving us the solution:
y = (12 - 2x) / 3
This can also be written as:
y = 4 - (2/3)x
This is the solution for 'y' in terms of 'x'. For any given value of 'x', you can substitute it into this equation to find the corresponding value of 'y'.
Method 2: Rearranging Terms
This method is essentially the same as Method 1 but emphasizes the rearranging of terms to isolate 'y'.
-
Start with the original equation: 2x + 3y = 12
-
Move the term with 'x' to the right side: Subtract 2x from both sides:
3y = 12 - 2x
-
Isolate 'y' by dividing both sides by 3:
y = (12 - 2x) / 3 or y = 4 - (2/3)x
This demonstrates that rearranging terms is a crucial aspect of solving for a specific variable.
Interpreting the Solution: y = 4 - (2/3)x
The solution y = 4 - (2/3)x represents a linear function. This means that the relationship between 'x' and 'y' is linear – a change in 'x' causes a proportional change in 'y'.
Slope and Intercept
The equation is in the slope-intercept form (y = mx + b), where:
-
m = -2/3 represents the slope of the line. The slope indicates the rate of change of 'y' with respect to 'x'. In this case, for every increase of 3 units in 'x', 'y' decreases by 2 units.
-
b = 4 represents the y-intercept. This is the point where the line intersects the y-axis (when x = 0). In this case, when x = 0, y = 4.
Graphing the Equation
Plotting this equation on a graph reveals a straight line with a negative slope, intersecting the y-axis at 4. This visual representation reinforces the understanding of the relationship between 'x' and 'y'.
Solving for Specific Values of x
The solution y = 4 - (2/3)x allows us to find the corresponding value of 'y' for any given value of 'x'. Let's consider some examples:
- If x = 0: y = 4 - (2/3)(0) = 4
- If x = 3: y = 4 - (2/3)(3) = 2
- If x = 6: y = 4 - (2/3)(6) = 0
- If x = -3: y = 4 - (2/3)(-3) = 6
These examples illustrate how the value of 'y' changes with 'x' according to the linear relationship defined by the equation.
Extending the Understanding: Systems of Equations
The equation 2x + 3y = 12 is often part of a system of equations. A system of equations involves multiple equations with the same variables. Solving a system of equations means finding the values of the variables that satisfy all equations simultaneously.
For example, consider the system:
2x + 3y = 12 x - y = 1
Solving this system requires using techniques like substitution or elimination to find the unique values of 'x' and 'y' that satisfy both equations. The solution for 'y' from 2x + 3y = 12 can be substituted into the second equation to solve for 'x', and vice-versa.
Applications in Real-World Scenarios
Solving linear equations like 2x + 3y = 12 has numerous practical applications:
- Economics: Modeling supply and demand, calculating costs and revenue.
- Physics: Determining relationships between variables like force, velocity, and acceleration.
- Engineering: Designing structures and systems, calculating material requirements.
- Computer Science: Creating algorithms and models, solving optimization problems.
- Business: Analyzing sales data, forecasting future trends.
Conclusion: Mastering Algebraic Techniques
Solving the equation 2x + 3y = 12 for 'y' is a fundamental skill in algebra. Understanding the methods, interpreting the solution, and recognizing its broader applications are crucial for success in various academic and professional fields. By mastering these techniques, you build a solid foundation for tackling more complex mathematical problems and developing a deeper understanding of quantitative relationships. The ability to isolate variables and interpret the resulting equations is a powerful tool for problem-solving and analysis across numerous disciplines. This article aimed not just to provide the answer but to foster a comprehensive understanding of the underlying principles and their wide-ranging implications. Remember to practice regularly to solidify your understanding and build your confidence in solving algebraic equations.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2x 3y 12 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.