20x 5y 15 Solve For Y
Greels
May 02, 2025 · 5 min read
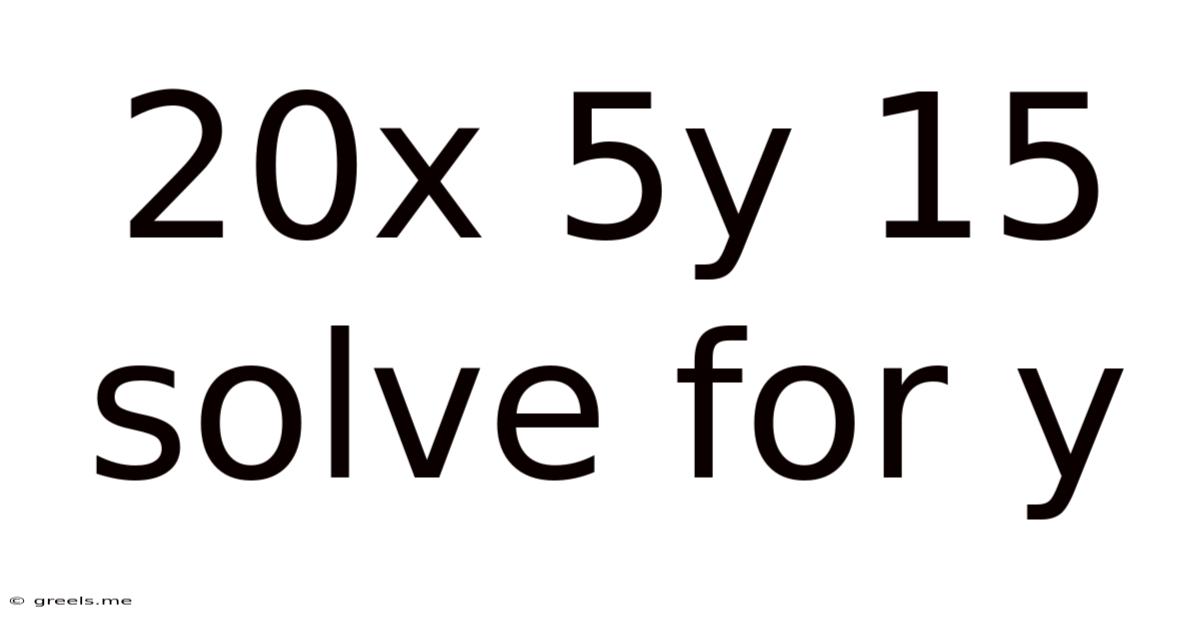
Table of Contents
Solving for 'y': A Comprehensive Guide to 20x + 5y = 15
This article provides a detailed explanation of how to solve the algebraic equation 20x + 5y = 15 for 'y'. We will explore various methods, including step-by-step solutions, alternative approaches, and practical applications. Understanding this process is fundamental to mastering algebraic manipulation and solving similar equations. We'll also delve into the significance of this equation in different mathematical contexts and explore related concepts.
Understanding the Equation: 20x + 5y = 15
The equation 20x + 5y = 15 is a linear equation in two variables, 'x' and 'y'. A linear equation represents a straight line when graphed on a coordinate plane. The goal is to isolate 'y' on one side of the equation, expressing it in terms of 'x'. This process is called solving for y. The solution will be an equation of the form y = mx + c, where 'm' represents the slope of the line and 'c' represents the y-intercept.
Method 1: Step-by-Step Solution for Solving 20x + 5y = 15
This method involves a series of algebraic manipulations to isolate 'y'.
-
Subtract 20x from both sides:
This step aims to move the term containing 'x' to the right-hand side of the equation. The equation becomes:
5y = -20x + 15
-
Divide both sides by 5:
To isolate 'y', we divide both sides of the equation by the coefficient of 'y', which is 5. This gives:
y = (-20x + 15) / 5
-
Simplify the expression:
We can simplify the right-hand side by dividing each term by 5:
y = -4x + 3
Therefore, the solution for 'y' is y = -4x + 3. This equation represents a straight line with a slope of -4 and a y-intercept of 3.
Method 2: Alternative Approach Using the Distributive Property
While the previous method is straightforward, we can also use the distributive property to simplify the equation before solving for 'y'. Observe that all the coefficients (20, 5, and 15) are divisible by 5.
-
Divide the entire equation by 5:
This simplifies the equation significantly:
(20x + 5y) / 5 = 15 / 5
This simplifies to:
4x + y = 3
-
Subtract 4x from both sides:
This isolates 'y':
y = -4x + 3
This alternative method yields the same solution: y = -4x + 3. This demonstrates that different algebraic approaches can lead to the same correct answer.
Graphical Representation and Interpretation
The solution, y = -4x + 3, represents a straight line on a Cartesian coordinate plane. The slope (-4) indicates the steepness and direction of the line, while the y-intercept (3) shows where the line crosses the y-axis. Graphing this equation allows for a visual understanding of the relationship between 'x' and 'y'. For every unit increase in 'x', 'y' decreases by 4 units.
Practical Applications and Real-World Examples
Linear equations like 20x + 5y = 15 have numerous applications in various fields:
-
Economics: This equation could represent a budget constraint, where 'x' represents the quantity of one good and 'y' represents the quantity of another, with a total budget of 15 units.
-
Physics: In physics, this equation might represent a relationship between two physical quantities, such as velocity and time.
-
Engineering: Linear equations are fundamental in engineering design and analysis, used to model relationships between different variables.
-
Business: In business, such equations can be used to model profit, cost, or revenue functions. For example, 'x' could represent the number of units sold and 'y' the profit generated.
Solving for 'x' – An Extension
While the primary focus was solving for 'y', it's also valuable to understand how to solve for 'x'. We can rearrange the original equation, 20x + 5y = 15, to solve for 'x':
-
Subtract 5y from both sides:
20x = -5y + 15
-
Divide both sides by 20:
x = (-5y + 15) / 20
-
Simplify the expression:
x = (-y/4) + (3/4)
Therefore, the solution for 'x' is x = (-y/4) + (3/4). This provides the expression for 'x' in terms of 'y'. Understanding both solutions allows for a complete understanding of the relationship between the two variables.
Exploring Related Concepts: Systems of Equations
This equation can also be part of a system of equations. A system of equations involves two or more equations with the same variables. Solving a system of equations means finding values of 'x' and 'y' that satisfy all the equations simultaneously. For example, if we had another equation, say 3x - y = 7, we could use methods like substitution or elimination to find the specific values of 'x' and 'y' that satisfy both equations.
Importance of Algebraic Manipulation Skills
The process of solving for 'y' in 20x + 5y = 15 emphasizes the importance of developing strong algebraic manipulation skills. These skills are essential not only in algebra but also in higher-level mathematics, science, and engineering. Proficiency in manipulating equations is crucial for problem-solving and critical thinking.
Conclusion: Mastering Linear Equations
Solving the equation 20x + 5y = 15 for 'y' demonstrates a fundamental algebraic concept with broad applications. Through step-by-step procedures and alternative approaches, we've shown that the solution, y = -4x + 3, represents a linear relationship between 'x' and 'y', easily graphed and interpreted. Understanding this process, along with related concepts like systems of equations, strengthens mathematical abilities and provides a foundation for tackling more complex problems. This knowledge is highly transferable to numerous fields, highlighting the practical significance of mastering linear algebra. Consistent practice and understanding of these techniques are key to success in mathematics and its related fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about 20x 5y 15 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.