2/5 Of A Number Is 16 What Is The Number
Greels
May 02, 2025 · 5 min read
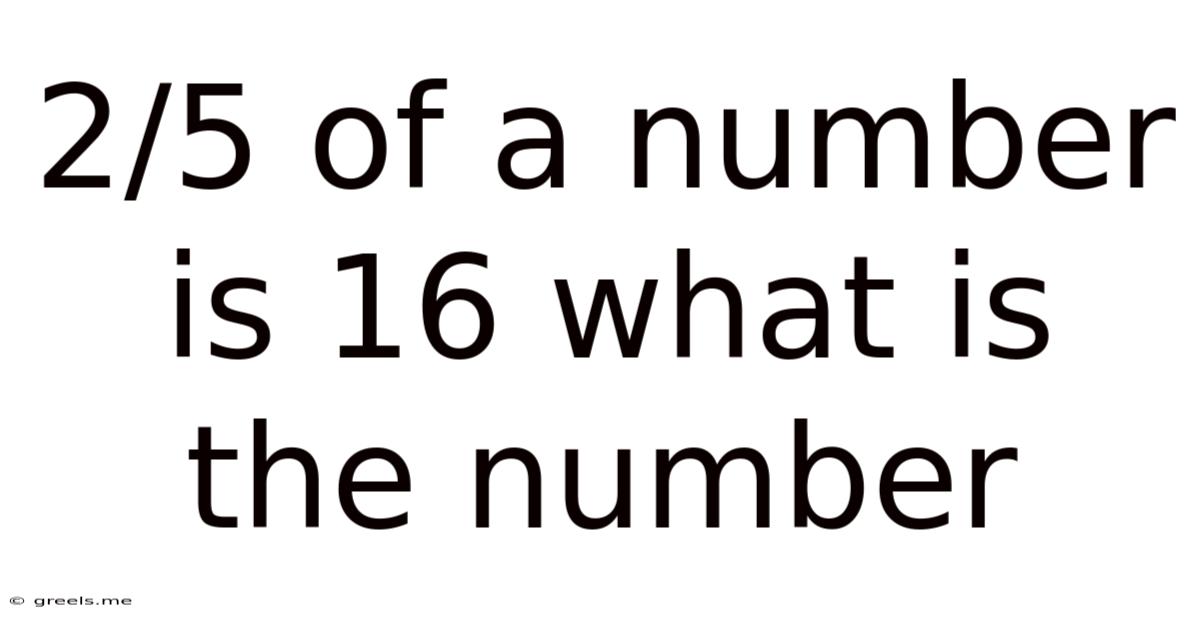
Table of Contents
2/5 of a Number is 16: What is the Number? A Comprehensive Guide to Solving Fraction Problems
This seemingly simple math problem, "2/5 of a number is 16; what is the number?", acts as a gateway to understanding fundamental concepts in algebra and fractions. While the solution might seem straightforward, exploring the various approaches to solving it reveals deeper insights into mathematical reasoning and problem-solving strategies. This comprehensive guide will not only provide the solution but also delve into different methods, explaining the underlying principles and offering practical applications for similar problems.
Understanding the Problem: Deconstructing the Question
Before diving into the solutions, let's break down the problem statement: "2/5 of a number is 16; what is the number?" This sentence translates into an algebraic equation. Let's represent the unknown number with the variable 'x'. The phrase "2/5 of a number" can be written as (2/5)x. The problem then becomes:
(2/5)x = 16
This equation forms the foundation for our various solution methods.
Method 1: Solving Using Inverse Operations
This is arguably the most straightforward method. The goal is to isolate the variable 'x' on one side of the equation. To do this, we'll use inverse operations. Since 'x' is being multiplied by 2/5, we'll perform the inverse operation: multiplication by the reciprocal. The reciprocal of 2/5 is 5/2.
-
Multiply both sides by the reciprocal: (5/2) * (2/5)x = 16 * (5/2)
-
Simplify: x = 80/2
-
Solve: x = 40
Therefore, the number is 40.
Verification: Checking Our Answer
It's crucial to verify our solution. Let's substitute x = 40 back into the original equation:
(2/5) * 40 = 16
Simplifying, we get:
80/5 = 16
16 = 16
The equation holds true, confirming that our solution, x = 40, is correct.
Method 2: Solving Using Cross-Multiplication
This method is particularly useful when dealing with proportions. We can rewrite the equation as a proportion:
2/5 = 16/x
Cross-multiplication simplifies the solution:
2 * x = 5 * 16
2x = 80
x = 40
Again, we arrive at the solution: x = 40. This method offers an alternative approach, highlighting the relationship between fractions and proportions.
Method 3: Solving Using Decimal Conversion
While the fraction method is often preferred for its clarity and precision, we can also solve this problem by converting the fraction to a decimal.
-
Convert the fraction to a decimal: 2/5 = 0.4
-
Rewrite the equation: 0.4x = 16
-
Solve for x: x = 16 / 0.4
-
Calculate: x = 40
This method demonstrates the flexibility of using decimal representations in solving algebraic equations.
Extending the Concepts: Similar Problems and Applications
The fundamental principles illustrated in this problem extend far beyond this specific example. Let's consider some variations and applications:
Problem Variation 1: Finding a Fraction of an Unknown Number
What if the problem was phrased differently? For example: "3/7 of a number is 21. What is the number?"
The approach remains the same. Let 'x' represent the unknown number. The equation becomes:
(3/7)x = 21
Following the inverse operation method:
x = 21 * (7/3) = 49
Therefore, the number is 49.
Problem Variation 2: Real-World Applications
This type of problem finds practical application in various real-world scenarios:
-
Percentage Calculations: Percentages are essentially fractions with a denominator of 100. If 20% of a number is 50, we can write this as (20/100)x = 50 and solve for x (resulting in x = 250).
-
Discount Calculations: If a store offers a 25% discount on an item, and the discount amount is $15, we can solve for the original price (x) using the equation (25/100)x = 15.
-
Proportion Problems: Many proportion problems can be solved using similar techniques. For instance, if 3 apples cost $2, how much will 9 apples cost? This can be set up as a proportion and solved using cross-multiplication.
-
Recipe Scaling: Scaling recipes up or down requires proportional reasoning similar to the principles applied in this problem. If a recipe calls for 2/3 cup of flour for 4 servings and you want to make 12 servings, you would solve a proportion to find the amount of flour needed.
Beyond the Basics: Developing Strong Problem-Solving Skills
Solving this seemingly simple equation allows us to practice and develop several crucial mathematical and problem-solving skills:
-
Algebraic manipulation: Understanding how to isolate variables and use inverse operations is fundamental to algebraic problem-solving.
-
Fraction manipulation: Working confidently with fractions, including finding reciprocals and performing multiplication and division, is essential.
-
Critical thinking: Understanding the problem statement and translating it into a mathematical equation requires critical thinking skills.
-
Verification and checking: Always verify your solution by substituting it back into the original equation. This is a crucial step in ensuring accuracy.
By mastering these techniques, you'll not only be able to solve similar fraction-based problems but also build a stronger foundation for tackling more complex mathematical concepts.
Conclusion: Mastering Fractions and Beyond
This detailed exploration of solving the problem "2/5 of a number is 16; what is the number?" extends beyond a simple arithmetic exercise. It unveils the fundamental principles of algebraic manipulation and proportional reasoning. The various methods presented – inverse operations, cross-multiplication, and decimal conversion – highlight the versatility and adaptability of mathematical techniques. Understanding these methods and applying them to different problem variations builds a robust foundation for tackling more complex mathematical challenges in various fields and real-world applications. Remember, practice is key. The more you work with these concepts, the more comfortable and proficient you will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2/5 Of A Number Is 16 What Is The Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.