2 3 3x 9 2 2x 6
Greels
Mar 28, 2025 · 5 min read
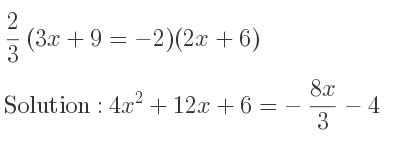
Table of Contents
Decoding the Sequence: 2 3 3x 9 2 2x 6 – A Deep Dive into Pattern Recognition and Mathematical Logic
The seemingly simple sequence "2 3 3x 9 2 2x 6" presents a fascinating puzzle, inviting us to explore the world of pattern recognition, mathematical logic, and the art of problem-solving. This article will delve into various approaches to understanding this sequence, examining potential patterns, logical structures, and the creative thinking involved in deciphering such cryptic arrangements. We’ll move beyond simply finding a solution to exploring why a particular solution might be preferred and the underlying principles at play.
Understanding the Nature of the Problem
Before diving into solutions, it's crucial to establish the nature of the problem. Is this a purely mathematical sequence? Could it represent a coded message? Are there hidden rules or constraints we need to uncover? The ambiguity allows for multiple interpretations, enriching the analytical process.
We'll initially assume a mathematical framework, exploring potential relationships between the numbers. The presence of "x" suggests multiplication might play a significant role, but the sequence's irregularity hints at a more complex pattern than simple arithmetic progression.
Exploring Potential Patterns and Relationships
Let's analyze the sequence meticulously: 2 3 3x 9 2 2x 6.
Analyzing the Numerical Components
The numbers themselves – 2, 3, 9, 6 – don't immediately reveal an obvious pattern. They're a mix of even and odd numbers, and there's no straightforward arithmetic progression (like addition or subtraction). However, we can explore various mathematical relationships:
-
Prime Factorization: Breaking down each number into its prime factors might uncover hidden connections. 2 is prime, 3 is prime, 9 is 3², and 6 is 2 x 3. This reveals a preponderance of 2s and 3s, hinting at a possible underlying structure based on these primes.
-
Multiplicative Relationships: The presence of "x" strongly suggests multiplication is involved. We can examine relationships between adjacent numbers, or perhaps groups of numbers, to explore multiplicative patterns. For example, is there a consistent relationship between the numbers before and after each "x"?
The Significance of "x"
The "x" symbols are critical. They unequivocally indicate multiplication operations. However, their placement isn't uniform, hinting at a more nuanced pattern than a simple alternating multiplication series. The position of each "x" might itself encode information, perhaps indicating a specific operation or rule to apply to the surrounding numbers.
We could consider the "x" as a separator between segments of the sequence, each requiring a unique operation to uncover the pattern. Alternatively, the "x" might denote a conditional operation, performed only under certain circumstances related to the surrounding numbers or their relationships.
Developing Hypothetical Solutions and Testing Them
Let's formulate a few hypotheses and test their validity:
Hypothesis 1: Segment-Based Operations
Let's divide the sequence into segments based on the "x" symbols: 2 3, 3x 9, 2 2x 6.
-
Segment 1 (2 3): Could there be a relationship like addition (2 + 3 = 5), subtraction (3 - 2 = 1), or multiplication (2 x 3 = 6)? None of these immediately provide a consistent pattern across all segments.
-
Segment 2 (3x 9): This is straightforward: 3 x 9 = 27.
-
Segment 3 (2 2x 6): This segment is more ambiguous. Possibilities include: 2 + 2 x 6 = 14; 2 x 2 + 6 = 10; 2 x (2 x 6) = 24; (2 + 2) x 6 = 24.
This hypothesis doesn't provide a cohesive, consistent pattern across all segments.
Hypothesis 2: Pattern based on Prime Factorization
Given the prevalence of 2s and 3s in the prime factorization, a solution might involve operations that utilize these prime factors. We could explore generating the next number in a sequence based on prime multiplication or addition of prime factors. This requires a degree of creativity and experimentation.
Hypothesis 3: A Coded Message
Could the sequence represent a coded message? The numbers might correspond to letters in the alphabet (A=1, B=2, etc.), symbols, or elements in a different code system. This approach requires a more extensive knowledge of coding and cryptography techniques and is outside the scope of a purely mathematical analysis.
Iterative Refinement and the Importance of Creative Problem-Solving
Solving this type of sequence puzzle often involves an iterative process:
- Observation: Carefully examine the sequence for any apparent patterns or relationships.
- Hypothesis Formation: Develop potential explanations or theories based on your observations.
- Testing: Evaluate your hypotheses by applying them to the sequence and seeing if they yield consistent results.
- Refinement: If your hypotheses are incorrect, refine them based on the feedback obtained during testing. This requires a significant amount of creative problem-solving skills.
- Iteration: Repeat this process until a satisfactory solution is found, or until it becomes clear that the puzzle requires additional information or a different approach.
The key to success lies in creative problem-solving. Don't be afraid to explore unconventional approaches or to experiment with different mathematical operations. The seemingly simple sequence "2 3 3x 9 2 2x 6" might be hiding a complex and elegant solution requiring innovative thinking and perseverance.
Expanding the Scope: Beyond Mathematical Analysis
While we've primarily focused on mathematical approaches, it's important to consider broader contexts. The sequence could represent:
- A fragment of a larger sequence: The provided segment might be just a part of a much longer pattern, requiring more data to identify the overall rule.
- Part of a more complex system: The sequence could be an element within a larger puzzle or system, where its meaning is revealed only in relation to other components.
- A deliberately ambiguous puzzle: The creator might have intentionally designed the sequence to be open to multiple interpretations, encouraging creative problem-solving.
Conclusion: The Enduring Appeal of Pattern Recognition
The sequence "2 3 3x 9 2 2x 6" serves as a microcosm of the broader challenge of pattern recognition. It highlights the importance of careful observation, creative hypothesis generation, iterative testing, and the rewarding feeling of uncovering a hidden structure or meaning. While definitive solutions may be elusive without additional information or context, the process of exploration itself is a valuable exercise in critical thinking and problem-solving. This puzzle demonstrates that even seemingly simple numerical sequences can hide surprisingly intricate patterns, rewarding those willing to delve into the depths of mathematical logic and the exciting world of pattern recognition. The key is persistence, a willingness to explore multiple approaches, and the embrace of creativity in problem-solving.
Latest Posts
Latest Posts
-
How Many Ounces Is 38 Grams
Mar 31, 2025
-
How Many Miles Is 160 Kilometers
Mar 31, 2025
-
How Many Pounds Is 11 Oz
Mar 31, 2025
-
What Is 120 Mm In Inches
Mar 31, 2025
-
How Much Is 48 Cm In Inches
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 2 3 3x 9 2 2x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
