2 2t 4 3 4 24 8t
Greels
Apr 02, 2025 · 5 min read
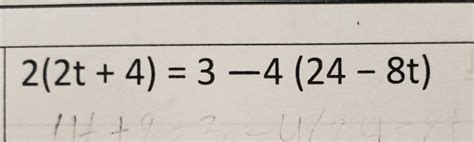
Table of Contents
Decoding the Sequence: 2 2t 4 3 4 24 8t – A Deep Dive into Pattern Recognition and Mathematical Logic
The seemingly random sequence "2 2t 4 3 4 24 8t" presents a fascinating challenge for those interested in pattern recognition and mathematical logic. At first glance, it appears chaotic. However, with careful observation and a systematic approach, we can uncover underlying patterns and potentially deduce a rule governing the sequence. This article will delve into various methods of analyzing this sequence, exploring different mathematical concepts and logical reasoning to unravel its mystery. We will consider multiple possibilities, acknowledging that there may be more than one valid solution, highlighting the importance of creative problem-solving in mathematics.
Understanding the Challenge: Numbers and Symbols
The immediate difficulty lies in the presence of both numbers and symbols ("t"). This immediately suggests that the sequence might not rely solely on arithmetic operations. We must consider the possibility of algebraic notation, symbolic representation, or even a combination of different mathematical concepts. The "t" could represent a variable, a constant, a function, or even an operation yet to be defined. This ambiguity introduces multiple avenues of exploration.
Methodical Approaches to Pattern Recognition
To systematically analyze the sequence, we can employ several strategies:
-
Difference Analysis: Calculating the differences between consecutive terms can reveal underlying arithmetic progressions or other patterns. This involves subtracting each term from the subsequent one. However, the presence of "t" immediately complicates this approach, as we cannot directly perform arithmetic operations involving an undefined symbol.
-
Ratio Analysis: Similar to difference analysis, we can examine the ratios between consecutive terms. This may expose geometric progressions or other multiplicative relationships. Again, the "t" term hinders a purely arithmetic approach.
-
Pattern Recognition through Grouping: Looking for patterns within subgroups of the sequence may reveal hidden structures. We could try grouping in pairs, triplets, or other combinations. For example, (2, 2t), (4, 3), (4, 24), (8t). This approach requires careful consideration of the "t" symbol and its potential interactions with the numbers.
-
Symbolic Logic and Algebraic Representation: We can attempt to assign meaning to "t" within an algebraic framework. Perhaps "t" represents a specific number, a function of preceding terms, or a symbolic operation. Exploring various possibilities through algebraic manipulation can potentially lead to a formula that generates the sequence.
-
Searching for Alternate Numerical Systems: The sequence might be using a different numerical system (base other than 10), a coding system, or involve specific mathematical functions or operations outside the typical arithmetic rules. The inclusion of "t" strongly suggests that this approach is worth exploring.
Exploring Potential Solutions and Interpretations
Let's explore some possible interpretations, keeping in mind the ambiguity inherent in the sequence:
Interpretation 1: "t" as a Constant
If we assume "t" represents a specific constant, we need to find a value of "t" that makes the sequence coherent. Let's try assigning a simple value, like "t = 1". This leads to the numerical sequence: 2, 2, 4, 3, 4, 24, 8. While there's no immediately obvious pattern, it opens the door for further analysis using difference or ratio methods or seeking an underlying function.
Interpretation 2: "t" as a Variable Dependent on the Sequence
This interpretation is more complex. "t" could represent a function of the preceding terms. We could speculate on a possible relationship, such as:
-
t = f(n), where 'n' is the index of the element in the sequence. This would allow "t" to vary based on its position. We could investigate if a simple arithmetic or polynomial function could fit the available data.
-
t = f(x_n), where 'x_n' refers to the previous terms in the sequence. This could mean "t" is a function of the immediate preceding term (or a combination of previous terms).
Determining the function 'f' would require testing various hypotheses and checking their consistency with the given sequence.
Interpretation 3: "t" as a Symbolic Operation
The "t" might represent a mathematical operation yet to be defined, acting on the preceding numbers. This option demands creative exploration of different operational possibilities. We could hypothesize operations like:
-
Concatenation: "t" might imply string concatenation. This would mean that, for example, 2t means the string "2" concatenated with "t", potentially converting it into a numerical representation later in the sequence. This would require defining rules for how the concatenated strings translate to numerical values within the sequence.
-
Modular Arithmetic: "t" might represent a modular operation. This would require specifying a modulus value and exploring how it affects the sequence's progression.
-
A newly defined mathematical operator: Perhaps "t" represents a completely novel operator, unique to this sequence, whose definition needs to be established through careful analysis.
Interpretation 4: Combination of Multiple Interpretations
The most likely scenario involves a combination of the aforementioned interpretations. For instance, "t" could represent a constant and a specific operation applied under certain conditions within the sequence. This requires a multi-faceted analysis and careful deduction.
The Importance of Context and Further Information
The challenge of deciphering this sequence highlights the critical role of context in problem-solving. Without additional information or clues, several valid interpretations could exist. To solve this definitively, we would need further terms in the sequence, or information on the underlying rules or principles that were used to generate this series. The limited number of terms (only 7), coupled with the presence of an undefined symbol, makes it impossible to guarantee a unique and definitive solution without further information.
Conclusion: The Art of Mathematical Discovery
Analyzing the sequence "2 2t 4 3 4 24 8t" is an exercise in pattern recognition, mathematical logic, and creative problem-solving. The presence of an undefined symbol introduces multiple potential interpretations, requiring a systematic investigation across diverse mathematical domains. While a definitive solution without more data remains elusive, the process of exploring different possibilities reveals the multifaceted nature of mathematical discovery and the value of persistent inquiry. The sequence serves as a potent reminder that mathematical problems don't always have a single, straightforward solution, and that creativity and a flexible approach are essential elements in unlocking their secrets. Further exploration of potential functions, operations, or interpretations remains a promising pathway for future researchers.
Latest Posts
Latest Posts
-
What Is 0 96 Rounded To The Nearest Tenth
Apr 03, 2025
-
How Many Cm In 54 Inches
Apr 03, 2025
-
How Many Pounds In 63 Kilos
Apr 03, 2025
-
How Many Lbs Is 95 Kg
Apr 03, 2025
-
What Is 40 Percent Of 1000
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 2 2t 4 3 4 24 8t . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
