10 Is 5 Of What Number
Greels
May 04, 2025 · 5 min read
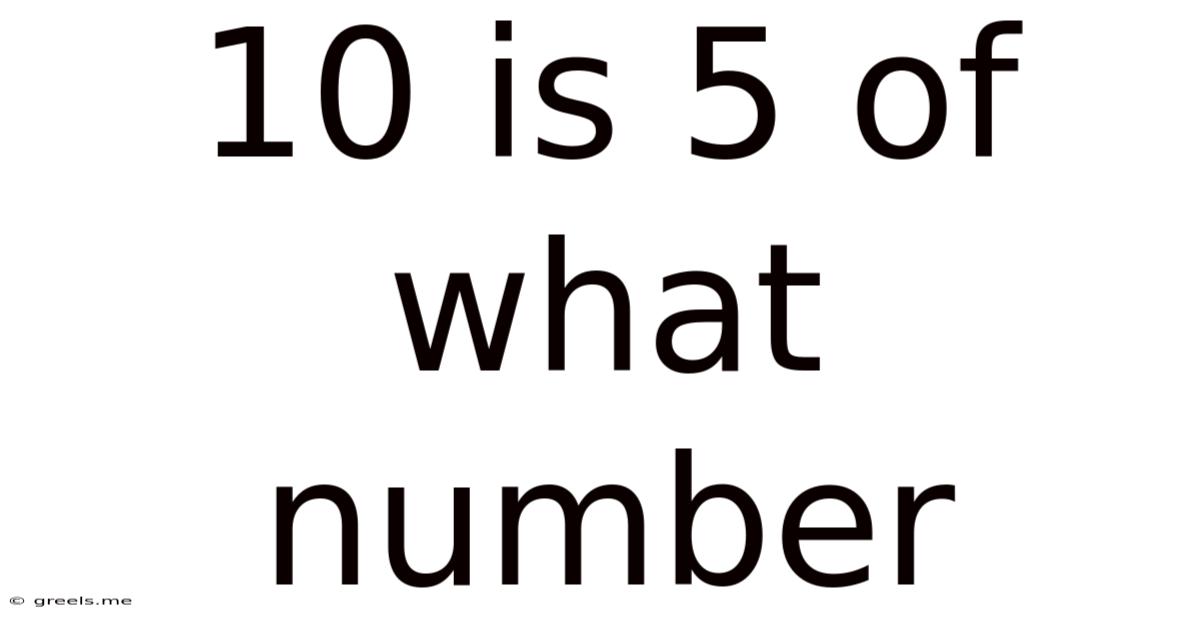
Table of Contents
10 is 50% of What Number? Unlocking the World of Percentages
This seemingly simple question, "10 is 50% of what number?", opens a door to a fundamental concept in mathematics: percentages. Understanding percentages is crucial not only for acing math tests but also for navigating everyday life, from calculating discounts at the mall to understanding financial reports. This comprehensive guide will not only answer the question directly but also delve into the underlying principles, providing you with the tools to solve similar problems and master the art of percentage calculations.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. This fundamental understanding is key to solving percentage problems.
Converting Percentages to Fractions and Decimals
To effectively work with percentages, it's essential to be able to convert them into fractions and decimals. Here's how:
- Percentage to Fraction: Divide the percentage by 100 and simplify the resulting fraction. For instance, 50% becomes 50/100, which simplifies to 1/2.
- Percentage to Decimal: Divide the percentage by 100. For example, 50% becomes 50 ÷ 100 = 0.5.
- Decimal to Percentage: Multiply the decimal by 100 and add the "%" symbol. For instance, 0.75 becomes 0.75 × 100 = 75%.
- Fraction to Percentage: Divide the numerator by the denominator, then multiply the result by 100 and add the "%" symbol. For example, 1/4 becomes (1 ÷ 4) × 100 = 25%.
Solving "10 is 50% of What Number?"
Now, let's tackle the original question: "10 is 50% of what number?" We can solve this using several methods.
Method 1: Using the Proportion Method
This method sets up a proportion, equating two ratios. We know that 10 is 50% of an unknown number (let's call it 'x'). We can write this as a proportion:
10/x = 50/100
To solve for x, we cross-multiply:
10 * 100 = 50 * x
1000 = 50x
x = 1000/50
x = 20
Therefore, 10 is 50% of 20.
Method 2: Using the Decimal Method
This method utilizes the decimal equivalent of the percentage. We know that 50% is equal to 0.5. We can set up the equation:
10 = 0.5 * x
To solve for x, we divide both sides by 0.5:
x = 10 / 0.5
x = 20
Again, we find that 10 is 50% of 20.
Method 3: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In our case, we know the part (10) and the percentage (50%). We need to find the whole (x). We can rearrange the formula:
Whole = (Part / Percentage) * 100
Substituting our values:
x = (10 / 50) * 100
x = 0.2 * 100
x = 20
Once more, the answer is 20.
Expanding Your Percentage Skills: Real-World Applications
Mastering percentage calculations opens up a world of practical applications. Here are some examples:
1. Calculating Discounts
Imagine a shirt is priced at $50 and is on sale for 20% off. To find the discount amount, we calculate 20% of $50:
Discount = 0.20 * $50 = $10
The final price after the discount is $50 - $10 = $40.
2. Determining Sales Tax
If the sales tax in your area is 8%, and you buy an item for $75, the sales tax amount is:
Sales Tax = 0.08 * $75 = $6
The total cost, including tax, is $75 + $6 = $81.
3. Understanding Financial Statements
Percentage changes are frequently used in financial reports to show growth or decline in profits, revenue, and expenses. For example, a company's revenue increased by 15% from the previous year. This indicates significant growth.
4. Calculating Tips
When dining out, calculating a tip is a common percentage application. To calculate a 15% tip on a $60 bill:
Tip = 0.15 * $60 = $9
5. Analyzing Statistics and Data
Percentages are extensively used in statistics to represent proportions and probabilities. Understanding percentages is crucial for interpreting data and making informed decisions based on statistical analysis.
Beyond the Basics: More Complex Percentage Problems
While the initial problem was straightforward, percentage problems can become more complex. Here are some examples and strategies to solve them:
1. Finding the Percentage Increase or Decrease
To find the percentage increase or decrease between two numbers, follow these steps:
- Find the difference between the two numbers.
- Divide the difference by the original number.
- Multiply the result by 100 to express it as a percentage.
For example, if a stock price increased from $20 to $25:
Difference = $25 - $20 = $5
Percentage Increase = (5 / 20) * 100 = 25%
2. Solving Problems with Multiple Percentages
Problems involving multiple percentages require a step-by-step approach. For example, if a price is increased by 10% and then decreased by 10%, the final price won't be the same as the original price due to the compounding effect. It's important to calculate each percentage change sequentially.
3. Dealing with Compound Interest
Compound interest involves earning interest on both the principal amount and accumulated interest. Calculating compound interest requires understanding exponential growth and using the appropriate formulas.
Mastering Percentages: Tips and Tricks
- Practice Regularly: Consistent practice is key to mastering percentage calculations. Work through various problems, starting with simple ones and gradually increasing the difficulty.
- Use Multiple Methods: Try different methods (proportion, decimal, formula) to solve the same problem. This will help you understand the underlying concepts more thoroughly and identify the method that works best for you.
- Visual Aids: Use diagrams or charts to visualize percentage problems. This can help clarify complex scenarios.
- Utilize Online Resources: Numerous online resources, including calculators and tutorials, can assist you in learning and practicing percentage calculations.
- Real-World Application: Apply percentage calculations to your daily life to reinforce your understanding and improve your practical skills.
Conclusion: The Power of Percentages
Understanding percentages is a valuable skill applicable in numerous aspects of life. From everyday shopping to complex financial analysis, mastering percentage calculations empowers you to make informed decisions and navigate the world with greater confidence. By mastering the fundamental concepts and practicing regularly, you can unlock the power of percentages and apply them effectively in various situations. Remember to break down complex problems into smaller, manageable steps, and don't hesitate to use different methods to find the solution that best suits your understanding. The journey to mastering percentages is a rewarding one, leading to a deeper understanding of numbers and their applications in the real world.
Latest Posts
Related Post
Thank you for visiting our website which covers about 10 Is 5 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.