1 2/3 Of The Number Is 4.75
Greels
May 03, 2025 · 5 min read
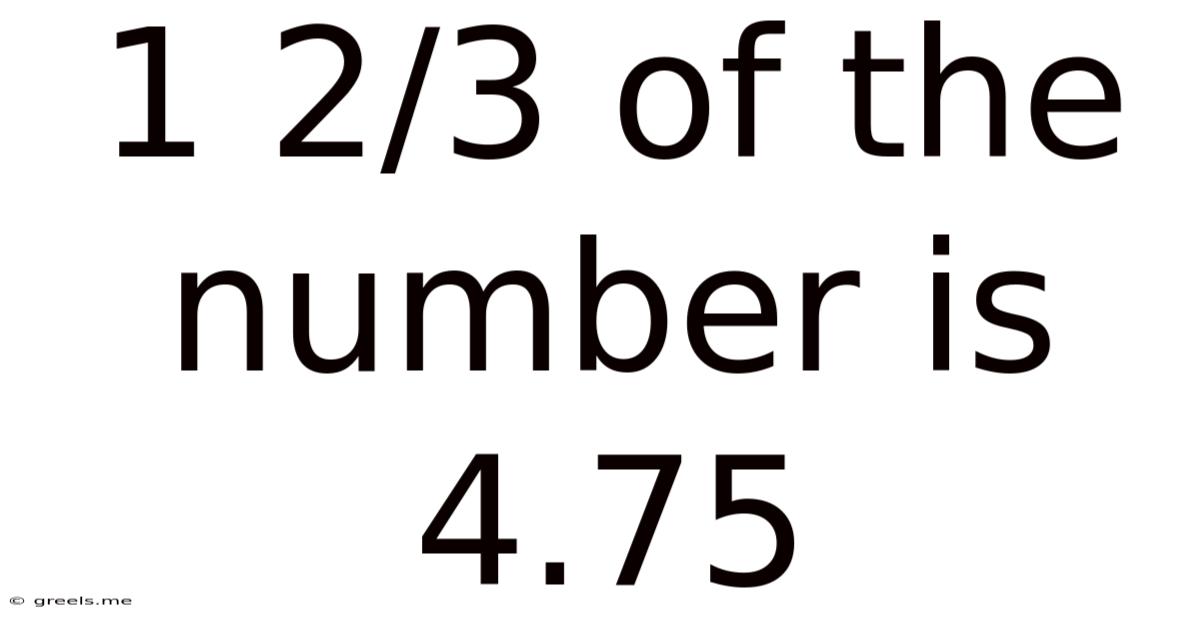
Table of Contents
1 2/3 of a Number is 4.75: Unraveling the Mathematical Mystery
Finding an unknown number when a fraction of it is known is a common mathematical problem. This article delves into the solution for the specific problem: "1 2/3 of a number is 4.75." We'll explore various methods to solve this, understand the underlying concepts, and even extend the problem to explore related scenarios. This comprehensive guide is designed to be accessible to a wide range of readers, from students strengthening their foundational math skills to those looking to brush up on their problem-solving abilities.
Understanding the Problem
The core of the problem lies in translating the given statement into a mathematical equation. The phrase "1 2/3 of a number" translates to 1 2/3 multiplied by the unknown number. We can represent the unknown number with a variable, let's say 'x'. The problem can then be written as:
(1 2/3) * x = 4.75
This equation is the key to finding the value of 'x'. We will explore multiple methods to solve this equation effectively.
Method 1: Converting to Improper Fraction
The first approach involves converting the mixed number 1 2/3 into an improper fraction. This simplifies the equation and makes it easier to solve.
1. Convert 1 2/3 to an improper fraction:
To convert 1 2/3 to an improper fraction, we multiply the whole number (1) by the denominator (3) and add the numerator (2). This result becomes the new numerator, while the denominator remains the same.
1 * 3 + 2 = 5
Therefore, 1 2/3 is equivalent to 5/3.
2. Rewrite the equation:
Our equation now becomes:
(5/3) * x = 4.75
3. Solve for x:
To isolate 'x', we multiply both sides of the equation by the reciprocal of 5/3, which is 3/5:
(3/5) * (5/3) * x = 4.75 * (3/5)
This simplifies to:
x = 4.75 * (3/5)
4. Calculate the result:
Now we perform the multiplication:
x = 2.85
Therefore, the number is 2.85.
Method 2: Converting to Decimal
Another approach involves converting both the mixed number and the given result into decimals. This method might be more intuitive for some individuals.
1. Convert 1 2/3 to a decimal:
We can convert 2/3 to a decimal by performing the division: 2 ÷ 3 = 0.666... (approximately 0.67). Adding the whole number 1, we get 1.67 (approximately). It's crucial to remember that this is an approximation, potentially leading to a slight inaccuracy in the final result.
2. Rewrite the equation:
The equation now looks like this:
1.67 * x ≈ 4.75
3. Solve for x:
To find 'x', we divide both sides of the equation by 1.67:
x ≈ 4.75 ÷ 1.67
4. Calculate the result:
Performing the division gives us an approximate value for x:
x ≈ 2.844
This method offers a slightly less precise answer due to the approximation of 2/3 as a decimal.
Method 3: Using Proportions
Proportions provide a powerful alternative method to solve this type of problem. We can set up a proportion based on the given information.
1. Set up the proportion:
We know that 1 2/3 (or 5/3) of 'x' is equal to 4.75. We can express this as a proportion:
(5/3) / 4.75 = 1 / x
2. Cross-multiply:
Cross-multiplying gives us:
5x = 3 * 4.75
3. Solve for x:
This simplifies to:
5x = 14.25
Dividing both sides by 5:
x = 2.85
This proportional method yields the same precise result as the improper fraction method.
Verification
To verify our solution, we can substitute the value of x (2.85) back into the original equation:
(1 2/3) * 2.85 = 4.75
(5/3) * 2.85 = 4.75
4.75 = 4.75
The equation holds true, confirming that our solution, x = 2.85, is correct.
Expanding the Problem: Real-World Applications
This seemingly simple mathematical problem has various real-world applications. Consider these scenarios:
-
Recipe Scaling: Imagine you have a recipe that calls for 1 2/3 cups of flour and yields 4.75 servings. To determine the amount of flour needed per serving, you would solve the equation (1 2/3) * x = 4.75.
-
Unit Conversion: You might be dealing with unit conversions where a specific fraction of a larger unit equals a known smaller unit.
-
Financial Calculations: Percentage-based calculations often involve similar equations. For example, finding the original price of an item after a discount is applied.
-
Construction & Engineering: Proportional scaling and measurements in construction or engineering projects utilize the same principles.
Common Mistakes to Avoid
When tackling such problems, several common errors can lead to inaccurate solutions:
-
Incorrect Fraction Conversion: Ensure accurate conversion of mixed numbers to improper fractions or decimals.
-
Order of Operations: Carefully follow the order of operations (PEMDAS/BODMAS) to avoid calculation errors.
-
Algebraic Errors: Pay attention to the rules of algebra when manipulating equations. For instance, remember to perform the same operation on both sides of the equation.
-
Rounding Errors: When using decimal approximations, understand the potential for rounding errors and their impact on the final result.
Conclusion
Solving the problem "1 2/3 of a number is 4.75" involves a straightforward application of algebraic principles. We've explored several methods – converting to improper fractions, converting to decimals, and using proportions – each providing a valid approach to finding the solution. Understanding these methods equips you to tackle similar problems effectively, broadening your problem-solving skills applicable to various real-world contexts. Remember to practice regularly to reinforce your understanding and improve your proficiency in solving such mathematical challenges. The key is to remain meticulous in your calculations and select the method most comfortable and efficient for you.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 2/3 Of The Number Is 4.75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.